World!Of
Numbers
HOME plate
WON |
The Nine Digits Page 4
with some Ten Digits (pandigital) exceptions
rood Page 1 rood Page 2 rood Page 3 rood Page 5 rood Page 6 rood Page 7 rood Page 8

When I use the term ninedigital in these articles I always refer to a strictly zeroless pandigital (digits from 1 to 9 each appearing just once).

Fourth Page

  Topic 4.7   [ November 17, 2025 ]
Concatenating prime factors of nine- & pandigitals
by Alexandru Petrescu

We start with a ninedigital and concatenating in ascending order the prime factors (counted without multiplicity or cwm).
From this decomposition we obtain another ninedigital. I found \(27\) solutions.
An example \(\to 152984367=3^2*29*586147\) which gives (cwm) \([3][29][586147]\) and \(329586147\) is a valid ninedigital.

Variations of the problem
From pandigital to pandigital produces \(184\) solutions, one of them \(4983621750\) having \(6\) prime factors.
From pandigital to ninedigital produces \(76\) solutions, one of them \(8634715920\) having \(6\) prime factors.
From ninedigital to pandigital produces \(19\) solutions.

Two interesting pairs
1. \(197342856\) and \(2*197342856=394685712\) produce the same ninedigital \(235694817\).
2. \(157348{\color{yellow}{0}}962~~[2][3][8741{\color{red}{5}}609]\) and \(157348962{\color{yellow}{0}}~~[2][3][{\color{red}{5}}][8741609]\) can be made equal by just shuffling two digits, \(0\) and \(5\).

Here is a handy table overview of all cases in a scrollbox.

Concatenating primefactors of nine- & pandigitals, taken without multiplicity
Concatenation
is a ninedigital		   Concatenation
is a pandigital		   Concatenation
is a ninedigital		   Concatenation
is a pandigital
9 digits → 9 digits   10 digits → 10 digits   10 digits → 9 digits   9 digits → 10 digits
1.  152984367  [3][29][586147]
2.  157624938  [2][3][8756941]
3.  168537492  [2][3][4681597]
4.  197248365  [3][5][17][28649]
5.  197342856  [2][3][569][4817]
6.  247693518  [2][3][4586917]
7.  267435891  [3][17][582649]
8.  295368174  [2][3][5469781]
9.  315249876  [2][3][8756941]
10.  325496817  [3][619][58427]
11.  356894712  [2][3][4956871]
12.  362589471  [3][89][452671]
13.  394685712  [2][3][569][4817]
14.  417528963  [3][487][95261]
15.  417928356  [2][3][647][5981]
16.  436917528  [2][3][71][85469]
17.  458621973  [3][61][278459]
18.  467253819  [3][251][68947]
19.  481753629  [3][7][2548961]
20.  481972356  [2][3][1487569]
21.  517628493  [3][61][942857]
22.  538927641  [3][7][2851469]
23.  678432159  [3][4261][5897]
24.  732948561  [3][467][58129]
25.  753621894  [2][3][4651987]
26.  921346785  [3][5][6824791]
27.  964287315  [3][5][7142869]
  
1.  1023485967  [3][7][16245809]
2.  1032865497  [3][2857][40169]
3.  1062749538  [2][3][19680547]
4.  1095734862  [2][3][60874159]
5.  1095742638  [2][3][60874591]
6.  1207843695  [3][5][26840971]
7.  1234697085  [3][5][4019][6827]
8.  1267938405  [3][5][28176409]
9.  1284965037  [3][2819][50647]
10.  1289405673  [3][5801][24697]
11.  1342765098  [2][3][74598061]
12.  1368975402  [2][3][76054189]
13.  1369702458  [2][3][76094581]
14.  1382547690  [2][3][5][1706849]
15.  1384926057  [3][59][2608147]
16.  1386247095  [3][5][10268497]
17.  1406875923  [3][5801][26947]
18.  1450783692  [2][3][5801][6947]
19.  1458360927  [3][67][2418509]
20.  1489507632  [2][3][17][608459]
21.  1529670843  [3][2861][59407]
22.  1573480962  [2][3][87415609]
23.  1573489620  [2][3][5][8741609]
24.  1574209638  [2][3][87456091]
25.  1574263098  [2][3][87459061]
26.  1624580973  [3][6047][29851]
27.  1625804397  [3][7][25806419]
28.  1627980543  [3][7][25840961]
29.  1629380745  [3][5][12069487]
30.  1630574298  [2][3][90587461]
31.  1637498520  [2][3][5][7][649801]
32.  1693542078  [2][3][94085671]
33.  1695837204  [2][3][47106589]
34.  1704962835  [3][5][47][806129]
35.  1723954680  [2][3][5][7][684109]
36.  1728536490  [2][3][5][6401987]
37.  1748509236  [2][3][48569701]
38.  1783024596  [2][3][16509487]
39.  1794538206  [2][3][71][468059]
40.  1804352697  [3][7][28640519]
41.  1840329765  [3][5][40896217]
42.  1934076582  [2][3][617][58049]
43.  1950864732  [2][3][54190687]
44.  1973408652  [2][3][54816907]
45.  1983267450  [2][3][5][1469087]
46.  2019357684  [2][3][641][87509]
47.  2039815764  [2][3][7][41][65809]
48.  2041897356  [2][3][18906457]
49.  2079814365  [3][5][46218097]
50.  2139705648  [2][3][14859067]
51.  2187436950  [2][3][5][4860971]
52.  2415083976  [2][3][4157][8069]
53.  2467195083  [3][487][562901]
54.  2473695018  [2][3][45809167]
55.  2481753960  [2][3][5][7][140689]
56.  2498573601  [3][281][509][647]
57.  2507643981  [3][509][182467]
58.  2518460793  [3][41][6825097]
59.  2574039681  [3][29][647][5081]
60.  2586319407  [3][7][41052689]
61.  2594073861  [3][61][4725089]
62.  2654137098  [2][3][49150687]
63.  2764308915  [3][5][61429087]
64.  2796483015  [3][5][20714689]
65.  2835691047  [3][7][5209][8641]
66.  2836150947  [3][7][45018269]
67.  2851940763  [3][7][45268901]
68.  2901567384  [2][3][5801][6947]
69.  2904876531  [3][79][4085621]
70.  2931745680  [2][3][5][4071869]
71.  2948536017  [3][7][46802159]
72.  2968037451  [3][29][47][80651]
73.  2973468501  [3][5087][21649]
74.  3059412867  [3][7][48562109]
75.  3146708952  [2][3][14568097]
76.  3186974205  [3][5][70821649]
77.  3215689407  [3][7][51042689]
78.  3248015697  [3][6217][58049]
79.  3451267089  [3][61][2095487]
80.  3452180796  [2][3][10654879]
81.  3486790521  [3][5081][76249]
82.  3497052168  [2][3][48570169]
83.  3571982640  [2][3][5][4961087]
84.  3586014792  [2][3][49805761]
85.  3589076412  [2][3][71][468059]
86.  3621498057  [3][59][6820147]
87.  3640825719  [3][47][2869051]
88.  3647912805  [3][5][81064729]
89.  3694701825  [3][5][16420897]
90.  3769425180  [2][3][5][6980417]
91.  3784165290  [2][3][5][4671809]
92.  3805162974  [2][3][70465981]
93.  3806927154  [2][3][70498651]
94.  3809576421  [3][7][20156489]
95.  3892140765  [3][5][86492017]
96.  4029375186  [2][3][74618059]
97.  4032918765  [3][5][89620417]
98.  4079631528  [2][3][7][41][65809]
99.  4095316872  [2][3][56879401]
100.  4107893256  [2][3][89][641057]
101.  4108963752  [2][3][57068941]
102.  4136529807  [3][89][5164207]
103.  4139056872  [2][3][57486901]
104.  4215960873  [3][269][580471]
105.  4270835619  [3][2897][54601]
106.  4397618520  [2][3][5][4071869]
107.  4562189730  [2][3][5][7][804619]
108.  4573269180  [2][3][5][8469017]
109.  4573891260  [2][3][5][8470169]
110.  4683971025  [3][5][20817649]
111.  4706315298  [2][3][41][708569]
112.  4780596321  [3][29][6105487]
113.  4830167952  [2][3][4157][8069]
114.  4912650783  [3][281][647509]
115.  4915760823  [3][61][8954027]
116.  4960712538  [2][3][91865047]
117.  4976810532  [2][3][46081579]
118.  4983621750  [2][3][5][41][89][607]
119.  5136280794  [2][3][10568479]
120.  5308274196  [2][3][49150687]
121.  5379124680  [2][3][5][4980671]
122.  5387460192  [2][3][18706459]
123.  5407693128  [2][3][75106849]
124.  5784301296  [2][3][40168759]
125.  5793261840  [2][3][5][8046197]
126.  5897136240  [2][3][5][8190467]
127.  5961403872  [2][3][17][405869]
128.  5982146073  [3][97][6852401]
129.  6039218475  [3][5][26840971]
130.  6124598703  [3][859][264071]
131.  6139478052  [2][3][56847019]
132.  6142975308  [2][3][56879401]
133.  6157904283  [3][29][7864501]
134.  6205719384  [2][3][86190547]
135.  6214790583  [3][409][562781]
136.  6230571948  [2][3][57690481]
137.  6308294715  [3][5][46728109]
138.  6329187504  [2][3][14650897]
139.  6431257089  [3][41][5809627]
140.  6457203981  [3][5107][46829]
141.  6519370824  [2][3][90546817]
142.  6521837904  [2][3][15096847]
143.  6534097281  [3][467][518209]
144.  6581792304  [2][3][45706891]
145.  6712304598  [2][3][479][86501]
146.  6837519420  [2][3][5][1406897]
147.  6851947302  [2][3][14098657]
148.  6912738450  [2][3][5][1706849]
149.  6974521308  [2][3][64578901]
150.  7031824596  [2][3][65109487]
151.  7038451692  [2][3][65170849]
152.  7143965280  [2][3][5][4961087]
153.  7153942608  [2][3][49680157]
154.  7168053249  [3][7][16254089]
155.  7324091856  [2][3][50861749]
156.  7403189562  [2][3][45698701]
157.  7604913852  [2][3][70415869]
158.  7610325948  [2][3][70465981]
159.  7621503948  [2][3][70569481]
160.  7894325610  [2][3][5][9746081]
161.  8129630745  [3][5][60219487]
162.  8146903725  [3][5][12069487]
163.  8162750943  [3][809][124567]
164.  8164702935  [3][5][60479281]
165.  8234791056  [2][3][57186049]
166.  8259134706  [2][3][59][864107]
167.  8479130652  [2][3][78510469]
168.  8527041396  [2][3][461][57089]
169.  8615072439  [3][17][2085469]
170.  8643219075  [3][5][12804769]
171.  9183764025  [3][5][40816729]
172.  9378520416  [2][3][10854769]
173.  9401782563  [3][61][5708429]
174.  9430716528  [2][3][65491087]
175.  9581074632  [2][3][14785609]
176.  9603218475  [3][5][42680971]
177.  9628351740  [2][3][5][7][849061]
178.  9670425381  [3][8629][41507]
179.  9760354821  [3][7][51642089]
180.  9760843251  [3][619][584027]
181.  9763480512  [2][3][16950487]
182.  9782534016  [2][3][167][50849]
183.  9801672435  [3][5][72604981]
184.  9814765302  [2][3][60584971]
  
1.  1027963584  [2][3][1784659]
2.  1045927836  [2][3][9684517]
3.  1048279563  [3][827][15649]
4.  1074869352  [2][3][1658749]
5.  1089357264  [2][3][7564981]
6.  1243869075  [3][5][1842769]
7.  1273890456  [2][3][5897641]
8.  1327509864  [2][3][6145879]
9.  1370425968  [2][3][9516847]
10.  1378254609  [3][29][586741]
11.  1386497520  [2][3][5][641897]
12.  1428937056  [2][3][4961587]
13.  1463298075  [3][5][2167849]
14.  1475068239  [3][71][256489]
15.  1589764032  [2][3][461][5987]
16.  1596748302  [2][3][9856471]
17.  1657093824  [2][3][59][48761]
18.  1697284530  [2][3][5][698471]
19.  1708236945  [3][5][4217869]
20.  1732840695  [3][5][4278619]
21.  1756924803  [3][7541][8629]
22.  1892357640  [2][3][5][194687]
23.  1930846275  [3][5][419][6827]
24.  1946730528  [2][3][6759481]
25.  2097684135  [3][5][1726489]
26.  2315907648  [2][3][59][68147]
27.  2403751869  [3][647][15289]
28.  2436189075  [3][5][461][7829]
29.  2480576931  [3][7][5624891]
30.  2564983017  [3][691][45827]
31.  2603419785  [3][5][6428197]
32.  2618705943  [3][7][4618529]
33.  2687359104  [2][3][41][56897]
34.  2715693480  [2][3][5][97][8641]
35.  2740851936  [2][3][9516847]
36.  2758406931  [3][7][6254891]
37.  2837091456  [2][3][47][61][859]
38.  2839704156  [2][3][8764519]
39.  2941860375  [3][5][2614987]
40.  3097568142  [2][3][647][9851]
41.  3175628409  [3][5741][6829]
42.  3179528064  [2][3][461][5987]
43.  3589021467  [3][967][45821]
44.  3697205184  [2][3][6418759]
45.  3860214975  [3][5][71][26849]
46.  3940682157  [3][59][274861]
47.  3958214607  [3][241][67589]
48.  4137982605  [3][5][41][27689]
49.  4170865392  [2][3][9654781]
50.  4319285760  [2][3][5][187469]
51.  4590813267  [3][67][845921]
52.  4658170923  [3][7][8215469]
53.  4790813526  [2][3][9857641]
54.  4801296375  [3][5][4267819]
55.  5091387264  [2][3][461][9587]
56.  5132608497  [3][6857][9241]
57.  5264078139  [3][2659][8147]
58.  5289037641  [3][257][84691]
59.  5679408312  [2][3][8764519]
60.  5974203168  [2][3][6914587]
61.  5987021364  [2][3][6159487]
62.  6891743250  [2][3][5][7][48619]
63.  7243591860  [2][3][5][496817]
64.  7486513920  [2][3][5][649871]
65.  7530419826  [2][3][5164897]
66.  7639214085  [3][5][6287419]
67.  7849215360  [2][3][5][7][64891]
68.  8359071264  [2][3][9674851]
69.  8634715920  [2][3][5][47][61][89]
70.  8940173625  [3][5][7946821]
71.  8961304752  [2][3][6914587]
72.  9140263875  [3][5][8124679]
73.  9378546120  [2][3][5][964871]
74.  9456178302  [2][3][6485719]
75.  9804215376  [2][3][7564981]
76.  9864730125  [3][5][47][62189]
   1.  192573846  [2][3][10698547]
2.  195238746  [2][3][10846597]
3.  195743862  [2][3][10874659]
4.  298513746  [2][3][16584097]
5.  375148962  [2][3][17][408659]
6.  381724965  [3][5][41][206897]
7.  385147692  [2][3][10698547]
8.  487921365  [3][5][10842697]
9.  532419687  [3][127][465809]
10.  725391846  [2][3][5801][6947]
11.  731856942  [2][3][40658719]
12.  793125486  [2][3][14687509]
13.  837942615  [3][5][18620947]
14.  913762854  [2][3][59][860417]
15.  915268347  [3][7][14528069]
16.  915832647  [3][47][2165089]
17.  962413857  [3][257][416089]
18.  974516238  [2][3][18046597]
19.  983125746  [2][3][54618097]
 
\\ Pari/gp code by A. Petrescu

\\ ninedigital --> ninedigital 27 solutions
\\
sss=0;for(n=1,9!,d=numtoperm(9,n+9!-1);a=sum(i=1,#d,d[i]*10^(#d-i));\
f=factor(a);k=#f[,1];s=sum(j=1,k,#digits(f[j,1]));\
if(s==9,v=[];v1=[];sv=Set(v);for(j=1,k,dd=digits(f[j,1]);\
sdd=Set(dd);sv=setunion(sv,sdd);v1=concat(v1,dd));\
if(#sv==9&&sv[1]>0,sss++;d1=fromdigits(v1);\
print(sss,". ",a,",",d1))))

\\ pandigital --> pandigital 184 solutions
\\
sss=0;for(k1=1,9*9!,d=numtoperm(10,k1+9!-1);\
a=sum(i=1,#d,(d[i]-1)*10^(#d-i));\
f=factor(a);k=#f[,1];s=sum(j=1,k,#digits(f[j,1]));\
if(s==10,v=[];v1=[];sv=Set(v);for(j=1,k,dd=digits(f[j,1]);\
sdd=Set(dd);sv=setunion(sv,sdd);v1=concat(v1,dd));\
if(#sv==10,sss++;d1=fromdigits(v1);print(sss,". ",a,","d1))))
   
\\ Pari/gp code by A. Petrescu

\\ pandigital --> ninedigital 76 solutions
\\
sss=0;for(k1=1,9*9!,d=numtoperm(10,k1+9!-1);a=sum(i=1,#d,(d[i]-1)*10^(#d-i));\
f=factor(a);k=#f[,1];s=sum(j=1,k,#digits(f[j,1]));\
if(s==9,v=[];v1=[];sv=Set(v);for(j=1,k,dd=digits(f[j,1]);\
sdd=Set(dd);sv=setunion(sv,sdd);v1=concat(v1,dd));\
if(#sv==9&&sv[1]>0,sss++;d1=fromdigits(v1);print(sss,". ",a,",",d1))))

\\ ninedigital --> pandigital 19 solutions
\\
sss=0;for(n=1,9!,d=numtoperm(9,n+9!-1);a=sum(i=1,#d,d[i]*10^(#d-i));\
f=factor(a);k=#f[,1];s=sum(j=1,k,#digits(f[j,1]));\
if(s==10,v=[];v1=[];sv=Set(v);for(j=1,k,dd=digits(f[j,1]);\
sdd=Set(dd);sv=setunion(sv,sdd);v1=concat(v1,dd));if(#sv==10,\
sss++;d1=fromdigits(v1);print(sss,". ",a,",",d1))))

Last term of (OEIS A358003) Least composite number k such that there are n digits in the intersection of the sets of digits of k and of the juxtaposition of prime factors of k (apart from multiplicity).
Ninth term of (OEIS A373645) The smallest number whose prime factor concatenation, as well as the number itself, when written in base n, contains all digits 0,1,...,(n-1).

  Topic 4.6   [ November 4, 2025 ]
Pandigitals as sum of a ninedigital and its reversal.

The smallest pandigital that is the sum of a ninedigital with its reversal is \(\bbox[2px,border:1px blue solid]{1034687529}\)

\(236145897+798541632\)

The largest pandigital that is the sum of a ninedigital with its reversal is \(\bbox[2px,border:1px blue solid]{1839526047}\)
\(864213579+975312468\)

In total there are \(320\) solutions but in fact each pandigital has \(8\to(\#24)\) or \(16\to(\#8)\) variations of sums of ninedigitals.
I'll explain later on. This leaves us with only \(\#32\) distinct pandigitals as solutions.
These variations comes from the fact that we can swap digits two by two. We take away some value just to be added/subtracted to the other side
leaving the sums unaltered. Here are two solutions with highlighting these swap digits. The outer and central digits do not take part in this swapping game!

\(\huge1034687529\)
\(\Large\color{yellow}{=}\)

\(\Large2{\color{red}{3}}{\color{green}{6}}{\color{blue}{1}}4{\color{blue}{5}}{\color{green}{8}}{\color{red}{9}}7\)
\(\Large\color{yellow}{+}\)
\(\Large7{\color{red}{9}}{\color{green}{8}}{\color{blue}{5}}4{\color{blue}{1}}{\color{green}{6}}{\color{red}{3}}2\)

   236145897 + 798541632
236541897 + 798145632
238145697 + 796541832
238541697 + 796145832
296145837 + 738541692
296541837 + 738145692
298145637 + 736541892
298541637 + 736145892
  

\(\huge1839526047\)
\(\Large\color{yellow}{=}\)

\(\Large8{\color{red}{6}}{\color{green}{4}}{\color{blue}{2}}1{\color{blue}{3}}{\color{green}{5}}{\color{red}{7}}9\)
\(\Large\color{yellow}{+}\)
\(\Large9{\color{red}{7}}{\color{green}{5}}{\color{blue}{3}}1{\color{blue}{2}}{\color{green}{4}}{\color{red}{6}}8\)

   864213579 + 975312468
864312579 + 975213468
865213479 + 974312568
865312479 + 974213568
874213569 + 965312478
874312569 + 965213478
875213469 + 964312578
875312469 + 964213578

We've got three columns where we can swap the digits making for \(2^3=8\) variations.
Eight pandigitals can be expressed with two sets of sums of ninedigitals making for \(2^4=16\) variations. An example :

\(\huge1639728045\)
\(\Large\color{yellow}{=}\)

\(\Large6{\color{red}{5}}{\color{green}{2}}{\color{blue}{3}}1{\color{blue}{4}}{\color{green}{7}}{\color{red}{8}}9\)
\(\Large\color{yellow}{+}\)
\(\Large9{\color{red}{8}}{\color{green}{7}}{\color{blue}{4}}1{\color{blue}{3}}{\color{green}{2}}{\color{red}{5}}6\)

and

\(\Large7{\color{red}{4}}{\color{green}{3}}{\color{blue}{2}}1{\color{blue}{5}}{\color{green}{6}}{\color{red}{9}}8\)
\(\Large\color{yellow}{+}\)
\(\Large8{\color{red}{9}}{\color{green}{6}}{\color{blue}{5}}1{\color{blue}{2}}{\color{green}{3}}{\color{red}{4}}7\)

   652314789 + 987413256
652413789 + 987314256
657314289 + 982413756
657413289 + 982314756
682314759 + 957413286
682413759 + 957314286
687314259 + 952413786
687413259 + 952314786

743215698 + 896512347
743512698 + 896215347
746215398 + 893512647
746512398 + 893215647
793215648 + 846512397
793512648 + 846215397
796215348 + 843512697
796512348 + 843215697

The following scrollbox shows all the solutions ordered from smallest to highest pandigitals.
The top fixed header is filled in with the Pari/gp code I wrote to achieve these results. 






\\ Pari/gp by Patrick De Geest
\\
{cnt=0; for(n=1,9!, d=numtoperm(9,n+9!-1);
rn1=0; for(i=1,9,rn1+=d[10-i]*10^(i-1));
rn2=fromdigits(Vecrev(digits(rn1))); duo=rn1+rn2; d=digits(duo);
if(#d==10 && prod(x=1,10,prime(d[x]+1))==6469693230 && rn1<rn2,
cnt+=1; print(cnt," - ",rn1," + ",rn2," = ",duo)));}


Ninedigital + ReversalPandigital Sum  


  


236145897 + 7985416321034687529


236541897 + 7981456321034687529


238145697 + 7965418321034687529


238541697 + 7961458321034687529


296145837 + 7385416921034687529


296541837 + 7381456921034687529


298145637 + 7365418921034687529


298541637 + 7361458921034687529


  


245136987 + 7896315421034768529


245631987 + 7891365421034768529


249136587 + 7856319421034768529


249631587 + 7851369421034768529


285136947 + 7496315821034768529


285631947 + 7491365821034768529


289136547 + 7456319821034768529


289631547 + 7451369821034768529


  


156324978 + 8794236511035748629


156423978 + 8793246511035748629


159324678 + 8764239511035748629


159423678 + 8763249511035748629


176324958 + 8594236711035748629


176423958 + 8593246711035748629


179324658 + 8564239711035748629


179423658 + 8563249711035748629


437126895 + 5986217341035748629


437621895 + 5981267341035748629


438126795 + 5976218341035748629


438621795 + 5971268341035748629


497126835 + 5386217941035748629


497621835 + 5381267941035748629


498126735 + 5376218941035748629


498621735 + 5371268941035748629


  


358124976 + 6794218531037546829


358421976 + 6791248531037546829


359124876 + 6784219531037546829


359421876 + 6781249531037546829


378124956 + 6594218731037546829


378421956 + 6591248731037546829


379124856 + 6584219731037546829


379421856 + 6581249731037546829


  


256314987 + 7894136521045728639


256413987 + 7893146521045728639


259314687 + 7864139521045728639


259413687 + 7863149521045728639


286314957 + 7594136821045728639


286413957 + 7593146821045728639


289314657 + 7564139821045728639


289413657 + 7563149821045728639


347215896 + 6985127431045728639


347512896 + 6982157431045728639


348215796 + 6975128431045728639


348512796 + 6972158431045728639


397215846 + 6485127931045728639


397512846 + 6482157931045728639


398215746 + 6475128931045728639


398512746 + 6472158931045728639


  


468213975 + 5793128641047526839


468312975 + 5792138641047526839


469213875 + 5783129641047526839


469312875 + 5782139641047526839


478213965 + 5693128741047526839


478312965 + 5692138741047526839


479213865 + 5683129741047526839


479312865 + 5682139741047526839


  


263145987 + 7895413621052687349


263541987 + 7891453621052687349


269145387 + 7835419621052687349


269541387 + 7831459621052687349


283145967 + 7695413821052687349


283541967 + 7691453821052687349


289145367 + 7635419821052687349


289541367 + 7631459821052687349


  


254136897 + 7986314521052768349


254631897 + 7981364521052768349


258136497 + 7946318521052768349


258631497 + 7941368521052768349


294136857 + 7586314921052768349


294631857 + 7581364921052768349


298136457 + 7546318921052768349


298631457 + 7541368921052768349


  


165324798 + 8974235611062748359


165423798 + 8973245611062748359


167324598 + 8954237611062748359


167423598 + 8953247611062748359


195324768 + 8674235911062748359


195423768 + 8673245911062748359


197324568 + 8654237911062748359


197423568 + 8653247911062748359


473126985 + 5896213741062748359


473621985 + 5891263741062748359


479126385 + 5836219741062748359


479621385 + 5831269741062748359


483126975 + 5796213841062748359


483621975 + 5791263841062748359


489126375 + 5736219841062748359


489621375 + 5731269841062748359


  


265314897 + 7984135621063728459


265413897 + 7983145621063728459


268314597 + 7954138621063728459


268413597 + 7953148621063728459


295314867 + 7684135921063728459


295413867 + 7683145921063728459


298314567 + 7654138921063728459


298413567 + 7653148921063728459


374215986 + 6895124731063728459


374512986 + 6892154731063728459


379215486 + 6845129731063728459


379512486 + 6842159731063728459


384215976 + 6795124831063728459


384512976 + 6792154831063728459


389215476 + 6745129831063728459


389512476 + 6742159831063728459


  


385124796 + 6974215831082546379


385421796 + 6971245831082546379


387124596 + 6954217831082546379


387421596 + 6951247831082546379


395124786 + 6874215931082546379


395421786 + 6871245931082546379


397124586 + 6854217931082546379


397421586 + 6851247931082546379


  


486213795 + 5973126841083526479


486312795 + 5972136841083526479


487213695 + 5963127841083526479


487312695 + 5962137841083526479


496213785 + 5873126941083526479


496312785 + 5872136941083526479


497213685 + 5863127941083526479


497312685 + 5862137941083526479


  


362157489 + 9847512631346908752


362751489 + 9841572631346908752


364157289 + 9827514631346908752


364751289 + 9821574631346908752


382157469 + 9647512831346908752


382751469 + 9641572831346908752


384157269 + 9627514831346908752


384751269 + 9621574831346908752


  


361254789 + 9874521631348706952


361452789 + 9872541631348706952


367254189 + 9814527631348706952


367452189 + 9812547631348706952


381254769 + 9674521831348706952


381452769 + 9672541831348706952


387254169 + 9614527831348706952


387452169 + 9612547831348706952


  


362145789 + 9875412631349687052


362541789 + 9871452631349687052


367145289 + 9825417631349687052


367541289 + 9821457631349687052


382145769 + 9675412831349687052


382541769 + 9671452831349687052


387145269 + 9625417831349687052


387541269 + 9621457831349687052


  


452136798 + 8976312541349768052


452631798 + 8971362541349768052


457136298 + 8926317541349768052


457631298 + 8921367541349768052


492136758 + 8576312941349768052


492631758 + 8571362941349768052


497136258 + 8526317941349768052


497631258 + 8521367941349768052


  


374126589 + 9856214731359748062


374621589 + 9851264731359748062


375126489 + 9846215731359748062


375621489 + 9841265731359748062


384126579 + 9756214831359748062


384621579 + 9751264831359748062


385126479 + 9746215831359748062


385621479 + 9741265831359748062


561324897 + 7984231651359748062


561423897 + 7983241651359748062


568324197 + 7914238651359748062


568423197 + 7913248651359748062


591324867 + 7684231951359748062


591423867 + 7683241951359748062


598324167 + 7614238951359748062


598423167 + 7613248951359748062


  


471256398 + 8936521741364908572


471652398 + 8932561741364908572


473256198 + 8916523741364908572


473652198 + 8912563741364908572


491256378 + 8736521941364908572


491652378 + 8732561941364908572


493256178 + 8716523941364908572


493652178 + 8712563941364908572


  


472153698 + 8963512741368504972


472351698 + 8961532741368504972


476153298 + 8923516741368504972


476351298 + 8921536741368504972


492153678 + 8763512941368504972


492351678 + 8761532941368504972


496153278 + 8723516941368504972


496351278 + 8721536941368504972


  


583124697 + 7964213851379546082


583421697 + 7961243851379546082


586124397 + 7934216851379546082


586421397 + 7931246851379546082


593124687 + 7864213951379546082


593421687 + 7861243951379546082


596124387 + 7834216951379546082


596421387 + 7831246951379546082


  


473215689 + 9865123741459728063


473512689 + 9862153741459728063


476215389 + 9835126741459728063


476512389 + 9832156741459728063


483215679 + 9765123841459728063


483512679 + 9762153841459728063


486215379 + 9735126841459728063


486512379 + 9732156841459728063


562314798 + 8974132651459728063


562413798 + 8973142651459728063


567314298 + 8924137651459728063


567413298 + 8923147651459728063


592314768 + 8674132951459728063


592413768 + 8673142951459728063


597314268 + 8624137951459728063


597413268 + 8623147951459728063


  


684213597 + 7953124861479526083


684312597 + 7952134861479526083


685213497 + 7943125861479526083


685312497 + 7942135861479526083


694213587 + 7853124961479526083


694312587 + 7852134961479526083


695213487 + 7843125961479526083


695312487 + 7842135961479526083


  


632157498 + 8947512361526908734


632751498 + 8941572361526908734


634157298 + 8927514361526908734


634751298 + 8921574361526908734


692157438 + 8347512961526908734


692751438 + 8341572961526908734


694157238 + 8327514961526908734


694751238 + 8321574961526908734


  


631254798 + 8974521361528706934


637254198 + 8914527361528706934


637452198 + 8912547361528706934


691254738 + 8374521961528706934


691452738 + 8372541961528706934


697254138 + 8314527961528706934


697452138 + 8312547961528706934


  


632145798 + 8975412361529687034


632541798 + 8971452361529687034


637145298 + 8925417361529687034


637541298 + 8921457361529687034


692145738 + 8375412961529687034


692541738 + 8371452961529687034


697145238 + 8325417961529687034


697541238 + 8321457961529687034


  


542136789 + 9876312451529768034


542631789 + 9871362451529768034


547136289 + 9826317451529768034


547631289 + 9821367451529768034


582136749 + 9476312851529768034


582631749 + 9471362851529768034


587136249 + 9426317851529768034


587631249 + 9421367851529768034


  


651324879 + 9784231561629748035


651423879 + 9783241561629748035


658324179 + 9714238561629748035


658423179 + 9713248561629748035


671324859 + 9584231761629748035


671423859 + 9583241761629748035


678324159 + 9514238761629748035


678423159 + 9513248761629748035


734126598 + 8956214371629748035


734621598 + 8951264371629748035


735126498 + 8946215371629748035


735621498 + 8941265371629748035


794126538 + 8356214971629748035


794621538 + 8351264971629748035


795126438 + 8346215971629748035


795621438 + 8341265971629748035


  


652314789 + 9874132561639728045


652413789 + 9873142561639728045


657314289 + 9824137561639728045


657413289 + 9823147561639728045


682314759 + 9574132861639728045


682413759 + 9573142861639728045


687314259 + 9524137861639728045


687413259 + 9523147861639728045


743215698 + 8965123471639728045


743512698 + 8962153471639728045


746215398 + 8935126471639728045


746512398 + 8932156471639728045


793215648 + 8465123971639728045


793512648 + 8462153971639728045


796215348 + 8435126971639728045


796512348 + 8432156971639728045


  


741256389 + 9836521471724908536


741652389 + 9832561471724908536


743256189 + 9816523471724908536


743652189 + 9812563471724908536


781256349 + 9436521871724908536


781652349 + 9432561871724908536


783256149 + 9416523871724908536


783652149 + 9412563871724908536


  


742153689 + 9863512471728504936


742351689 + 9861532471728504936


746153289 + 9823516471728504936


746351289 + 9821536471728504936


782153649 + 9463512871728504936


782351649 + 9461532871728504936


786153249 + 9423516871728504936


786351249 + 9421536871728504936


  


853124679 + 9764213581829546037


853421679 + 9761243581829546037


856124379 + 9734216581829546037


856421379 + 9731246581829546037


873124659 + 9564213781829546037


873421659 + 9561243781829546037


876124359 + 9534216781829546037


876421359 + 9531246781829546037


  


864213579 + 9753124681839526047


864312579 + 9752134681839526047


865213479 + 9743125681839526047


865312479 + 9742135681839526047


874213569 + 9653124781839526047


874312569 + 9652134781839526047


875213469 + 9643125781839526047


875312469 + 9642135781839526047

  Topic 4.5   [ July 4, 2005 ]
More Ninedigital Powers
by Peter Kogel

" Hi Patrick,
Herewith is another pandigital 'project' that I investigated some while ago.

Notable results include:

213452 + 87962 = 532978641

The first term contains 1...5 and the second term contains 6...9.

25382 + 176492 = 29432 + 175862 = 317928645

Only example where two sums are equal.

5393 + 2463 + 7183 = 541623987
5393 + 4623 + 7183 = 625348179

The above is what I call a 'pandigital amicable pair' (see below).

274 + 354 + 684 + 1494 = 516297843
274 + 354 + 864 + 1494 = 549617283

Only one term on the left hand side is different.

95 + 175 + 265 + 435 + 585 = 816725493

Only example for 5th power.

Kind regards,
Pete Kogel. "

Pandigital diversions concerning a1P + a2P + ... + apP = N    [ P ⩾ 2 ]

P = 2 A2 + B2 = N

E.g.:

15962 + 248372 = 619423785

In the above, the numbers A & B combined and also the result on the right hand side
contain the digits 1...9 (zero-less pandigital).

There are 78 such solutions ¬

A      B
A      B
A      B
A      B
1596   24837
1635   29487
1875   24693
2367   19485
2436   18975
2538   17649
2784   15369
2943   17586
3495   12768
3516   28479
3654   12897
3846   29175
3864   25179
3915   28467
3984   26715
4197   25638
4359   16278
4395   27186
4536   12987
4698   21357
4857   21396
4896   21753
4965   17382
4968   15237
5367   14928
5376   12984
5376   18429
5436   17289
5469   13728
5496   18237
5613   27948
5679   14238
5697   21384
5763   21948
5964   18273
5976   21483
6189   25374
6198   23547
6345   21987
6453   19287
6459   17328
6471   23589
6471   29538
6528   13749
6549   27831
6813   24597
6831   29745
6945   13782
6975   14823
7164   25983
7356   24189
7359   28146
7431   29658
7458   23619
7659   13248
7659   13428
7824   19356
7863   21495
7869   23514
7953   16824
8259   13476
8295   14763
8349   17562
8352   17469
8517   29643
8745   16392
8793   12546
8796   21345
8796   23541
8934   15267
8973   12546
8976   25413
9156   27483
9168   23475
9627   18543
9687   24513
9735   24861
9741   26358

Observations

There are only 5 examples where A or B appears in more than one solution: viz ¬

53762 + 129842 = 197485632
53762 + 184292 = 368529417

64712 + 235892 = 598314762
64712 + 295382 = 914367285

76592 + 132482 = 234169785
76592 + 134282 = 238971465

87962 + 213452 = 532978641
87962 + 235412 = 631548297

87932 + 125462 = 234718965
89732 + 125462 = 237916845

There are several examples where simply swapping two digits in A leads to a member of another solution ¬
E.g.:

4359 4395
5469 5496
5679 5697
Etc.

213452 + 87962 = 532978641

In the solution above, A contains the digits 1...5 and B contains the digits 6...9

25382 + 176492 = 29432 + 175862 = 317928645

The above is the only example where N is duplicated.

P = 3 A3 + B3 + C3 = N

E.g.:

1233 + 4653 + 8973 = 824139765

A, B & C combined and N are zero-less pandigital.

There are 101 solutions; viz ¬

A     B     C
A     B     C
A     B     C
A     B     C
123   465   897
124   389   576
124   635   789
124   639   875
126   593   784
128   634   759
129   375   468
129   365   847
132   479   865
135   297   684
136   582   749
137   286   954
138   259   746
138   264   795
139   576   824
142   396   857
145   297   863
145   296   873
145   693   728
146   397   825
147   265   983
149   258   637
153   469   728
156   492   738
159   423   768
162   354   789

165   324   789
165   234   978
167   532   894
172   348   596
175   629   843
176   549   832
178   426   593
182   379   564
184   527   936
186   395   742
189   246   537
192   548   763
192   356   847
193   468   572
194   285   736
194   376   825
194   627   835
196   273   458
196   342   785
197   364   825
198   243   675
213   467   589
213   578   649
215   378   496
216   397   485
216   387   495

219   438   567
219   436   587
231   456   789
234   619   857
237   654   819
246   539   718
249   381   675
251   486   739
253   419   768
254   391   768
258   314   697
259   641   837
261   457   938
267   384   951
269   537   841
271   398   546
271   458   639
274   591   863
278   351   496
279   413   856
312   479   658
317   489   526
318   547   692
321   498   576
321   564   897
328   519   674

342   596   871
351   468   792
362   459   718
372   519   864
374   526   918
378   512   649
381   469   572
386   519   724
394   561   728
397   458   621
398   415   672
418   693   725
429   576   831
429   671   835
462   539   718
483   597   621
487   521   693
489   613   725
493   581   627
493   512   786
514   639   782
574   639   812
591   624   738

While looking through the above list I noticed that some values occur in more than one solution
and I wondered whether I could chain several such solutions together; wherein the last number
becomes the first number in the next link: e.g. ¬

(123, 465, 897)
          (897, 321, 564) 
                    (564, 182, 379)

A slightly longer chain would be ¬

(193, 468, 572)
          (572, 381, 469)
                    (469, 153, 728)
                              (728, 693, 145)
                                        (145, 296, 873)

The longest chain that I found consists of 24 members ¬

(172, 348, 596) , (596, 871, 342) , (342, 785, 196) , (196, 273, 458) , (458, 271, 639) ,
(639, 875, 124) , (124, 389, 576) , (576, 831, 429) , (429, 671, 835) , (835, 194, 627) ,
(627, 581, 493) , (493, 786, 512) , (512, 649, 378) , (378, 215, 496) , (496, 278, 351) ,
(351, 792, 468) , (468, 193, 572) , (572, 381, 469) , (469, 153, 728) , (728, 145, 693) ,
(693, 418, 725) , (725, 613, 489) , (489, 317, 526) , (526, 918, 374)

This chain was found by 'hand' so it is possible that I may have missed a longer chain.

While searching for the above I came across the following nine-member 'pandigital sociable group'
i.e. the last member can be chained with the very first member.

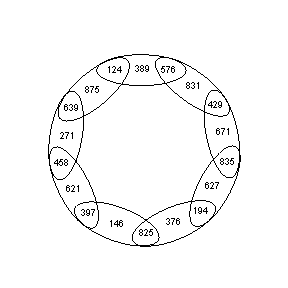(124, 389, 576)
(576, 831, 429)
(429, 671, 835)
(835, 627, 194)
(194, 376, 825)
(825, 146, 397)
(397, 621, 458)
(458, 271, 639)
(639, 875, 124)

There is also one example of a 'pandigital amicable pair'.

(539, 246, 718)
          (718, 462, 539)
Other notable curiosities
(123, 564, 879) & (124, 639, 875)
  |    |    |       |    |    |
(231, 465, 897)	& (142, 396, 857)
The digits in A, B & C are permuted. 
(231, 456, 789)
B & C contain the series 456_789 in order.
(394, 561, 728) = (394, 394+167, 394+167+167)
A, B, C are in arithmetic progression (difference = 167).

P = 4 A4 + B4 + C4 + D4 = N

E.g.:

244 + 694 + 784 + 1354 = 824139765

A, B, C & D combined and N are zero-less pandigital.

There are only 5 solutions; viz ¬

244 + 694 + 784 + 1354 = 392164578
274 + 354 + 684 + 1494 = 516297843
274 + 354 + 864 + 1494 = 549617283
484 + 574 + 964 + 1234 = 329685714
644 + 724 + 854 + 1394 = 469152738

The second and third solutions shown above are particularly noteworthy (another 'pandigital amicable pair').

P = 5 A5 + B5 + C5 + D5 + E5 = N

95 + 175 + 265 + 435 + 585 = 816725493

The above is the only solution.

P ⩾ 6 AP + BP + CP + DP + EP + FP + ... = N

No solutions.

  Topic 4.4   [ March 24, 2005 ]
The Unique Pandigital 3816547290
by John Morse

" In the header of this message is 3,816,547,290 which is the only 10-digit
pandigital number whose first N digits are a multiple of N. I first discovered
that in The Dictionary of Curious and Interesting Numbers by David Wells,
and I wrote an explanation of how one could figure out that is the number.

John Morse
Albany New York USA "

Mathematics Puzzle

Find the one and only 10-digit number such that :

1) All digits are different, and
2) the number formed by the first N digits is divisible by N.

This explanation is my own, but I first learned about the amazing
mystery number (381,654,729) in an entertaining book, one of my ten
favorite math-themed books of all time :

Wells, David. "The Penguin Book of Curious and Interesting Numbers"
(New York, New York: Penguin Putnam, Inc., 1997, page 185).

Procedure

Let the letters A thru J stand for the digits of the number. Then :

A B C D E F G H I J is the mystery number, whereas :

AB is evenly divisible by 2,
ABC is evenly divisible by 3,
ABCD is evenly divisible by 4,
ABCDE is evenly divisible by 5,
ABCDEF is evenly divisible by 6,
ABCDEFG is evenly divisible by 7,
ABCDEFGH is evenly divisible by 8,
ABCDEFGHI is evenly divisible by 9,
ABCDEFGHIJ is evenly divisible by 10.

A number is evenly divisible by 10 only if its last digit is zero.

Hence, we have found right away that J must equal zero, since the
ten-digit number ends in that digit J.

What about divisibility by 9 ? This particular number takes care of that
matter because its nine-digit 'fragment' ABCDEFGHI must use one each of
digits 1 thru 9, and the sum of the nine digits is 45, which is a multiple of 9.

A number is evenly divisible by 9 if the sum of its digits is 9 or a
multiple of 9 itself. Hence, ANY arrangement of the digits 1 thru 9
(or 0 thru 9), each digit used exactly once, will always result in the
number being a multiple of 9.

A number is evenly divisible by 5 only if its last digit is a five or
a zero.

Since all the digits of ABCDEFGHIJ are different, we cannot use zero
since J already has that value.

The first five digits of the entire number are ABCDE, hence digit E
must be 5.

So far, the mystery number looks like this :

A B C D 5 F G H I 0

Even numbers only are evenly divisible by even divisors, e.g., if you
want to divide some number N by 2 or 4 or 6, etc., that number N must
be even since dividing an odd number by an even number will always leave
(an odd) remainder.

Hence, consider the mystery number's even-numbered digits. They
correspond to letters B, D, F, and H. Since zero is being used for J, the
even digits 2, 4, 6, and 8 must correspond to those other four letters.

Therefore, the remaining letters in the number - A, C, G, and I - must
stand for odd digits.

Because the odd digit 5 is already in use via the letter E, A can only
be 1, 3, 7, or 9. The same restrictions apply to C, G, and I.

There are many ways that AB is evenly divisible by 2 : merely let B
equal 2 or 4 or 6 or 8. Hence, there are too many possible ways so
far to assign digits for A and B. How about ABC, which must be a
multiple of 3 ?

The digits A + B + C must add up to a multiple of 3, and in this
instance, B is the only even digit. Hence, the following trios are possible
for fragment ABC :

123 129 147 183 189 321 327 369 381
387 723 729 741 783 789 921 927 963

Eighteen possible permutations exist for ABC; it looks like a lot of
trial and error lies ahead if we test all these 3-digit groups in
combination with the remaining digits for D, F, G, and H. (It does not
matter yet what digit I must be, since the entire 9-digit number up to I
is already divisible by 9.)

However, note that the four-digit fragment ABCD must be a multiple of 4,
and this is possible only if the number formed by the last two digits -
here, CD - is a multiple of 4.

Since C is odd, D can only be 2 or 6. If we try 4 or 8 instead for D, then we
get numbers such as 18, 34, 78, or 94 - none of which are evenly divisible by 4.

A similar situation arises for the 8-digit fragment ABCDEFGH. Since G
is odd, H can only be 2 or 6. A number is divisible by 8 only if its
last three digits (here, FGH) is evenly divisible by 8.

So, between them, D and H use up the digits 2 and 6. We are not sure
which letter will have which digit, but we can eliminate the 3-digit
fragments above where B happens to be 2 or 6, leaving these possible
permutations for the digit group ABC :

147 183 189 381 387 741 783 789

Good. Number of permutations is now only eight instead of eighteen.

Since B and F must be even, they must use the only remaining even
digits - 4 and 8 - between them. Let's take a look at the mystery
number where we assign the digits 2 and 6 to D and H and the digits
4 and 8 to B and F :

A4C258G6I0
A4C658G2I0
A8C254G6I0
A8C654G2I0

Consider the six-digit fragment ABCDEF. Its digits must add up to a multiple
of 3. All multiples of six are even, but we already know that F must be even.

Since the digits ABC add up to a multiple of 3, so must those in fragment
DEF. Since E is 5, only two possibilities exist for digits in DEF :

258 654

So, we can eliminate two of the four 10-digit numbers above, leaving :

A4C258G6I0
A8C654G2I0

Let's take another look at the 8-digit fragment ABCDEFGH and see if we
can determine whether F must be 4 or 8.

If D=2, then B must be 4, F must be 8, and H must be 6. Since FGH must
be a multiple of 8, it could only end in the following three digits :

816 836 876 896

Of these four 3-digit numbers, 836 and 876 are NOT multiples of 8, so
eliminate them, leaving only 816 and 896 for FGH.

If D=6, then B must be 8, F must be 4, and H must be 2. Since FGH must
be a multiple of 8, it could only end in the following three digits :

412 432 472 492

Of these four 3-digit numbers, 412 and 492 are NOT multiples of 8, so
eliminate them, leaving only 432 and 472 for FGH.

Hence, possible arrangements of digits in the mystery number could be :

[1] A4C25816I0
[2] A4C25876I0
[3] A8C65432I0
[4] A8C65472I0

Recall that fragment ABC must be a multiple of 3. In choice [1], the
only available digits for A and C are 3, 7, and 9. No combination of
these digits will enable ABC to be a multiple of 3, so eliminate choice [1].

For choice [2], the only digits available are 1, 3, and 9. No combination
of these will make ABC a multiple of 3, so scratch choice [2].

For choice [3], the only digits left are 1, 7, and 9. The only workable
combination that will make ABC a multiple of 3 is when neither A nor C
is 7, so I must be 7.

For choice [4], the only digits available are 1, 3, and 9. Digits
1 and 3 may represent A and C, in which case I must be 9. If digits
1 and 9 stand in for A and C, then I must be 3.

So, two choices for the mystery number were removed, leaving these
possible configurations for the mystery number :

[1] 1896543270
[2] 9816543270
[3] 1836547290
[4] 3816547290
[5] 1896547230
[6] 9816547230

Almost there! Each of these six numbers is such that the number AB is
divisible by 2, ABC by 3, ABCD by 4, ABCDE by 5, ABCDEF by 6, ABCDEFGH
by 8, ABCDEFGHI by 9, and ABCDEFGHIJ by 10.

What about the fragment ABCDEFG ? Is it divisible by 7 ? Test each of
the six numbers above using their first seven digits :

[1] 1896543 divided by 7 leaves remainder 5. nope.
[2] 9816543 divided by 7 leaves remainder 2. nope.
[3] 1836547 divided by 7 leaves remainder 6. nope.
[4] 3816547 divided by 7 leaves remainder 0. YES !
[5] 1896547 divided by 7 leaves remainder 2. nope.
[6] 9816547 divided by 7 leaves remainder 6. nope.

Aha! Only choice [4] leaves no remainder when its fragment ABCDEFG is
divided by 7.

Finally we found the mystery number ! It is

3 8 1 6 5 4 7 2 9 0

Are all the digits different ? Yes. A number with that property is
known as "pandigital". The prefix "pan-" means "all".

How about divisibility of the first N digits by N ? Check and see :

38 divided by 2 = 19, no remainder. Yawn.
381 divided by 3 = 127, no remainder. Okay.
3816 divided by 4 = 954, no remainder. Okay!
38165 divided by 5 = 7633, no remainder. Big deal.
381654 divided by 6 = 63609, no remainder. Good.
3816547 divided by 7 = 545221, no remainder. Good!
38165472 divided by 8 = 4770684, no remainder. Great!
381654729 divided by 9 = 42406081, no remainder. Of course.
3816547290 divided by 10 = 381654729, no remainder. Wonderful!!!

There is no other 10-digit number whose first N digits are evenly
divisible by N - and where every digit occurs once !

Other internet sources discussing this topic :
http://ken.duisenberg.com/potw/archive/arch96/960919sol.html
http://www.nrich.maths.org.uk/public/viewer.php?obj_id=796&part=solution&refpage=viewer.php
http://begghilos2.ath.cx/~jyseto/Academia/Math-Problem-2.php
http://www.rodoval.com/heureka/probsnum.html
... many more when 3816547290 is entered as keyword in GOOGLE for instance !


  Topic 4.3   [ February 27, 2005 ]
Nine and Ten digit squares
by Peter Kogel

" I've had a fascination for numbers and rec maths ever since I first read
Martin Gardner's column in Scientific American many years ago. My particular
fascination is for nine and ten digit number patterns and I've found your
excellent website the source of much inspiration.

This project has been to investigate patterns along the lines of 99066^2
( 9814072356 ) and have found some interesting results that you might like.

Some highlights

77772277772 = 60485271895340361729

The square contains each digit 0...9 twice and the square root is a rather
particular palindrome.

42539071862 = 1809572634_7102438596

The lefthand side is pandigital and the square on the righthand side contains
the digits 0...9 repeated in each half (there are two other such examples).

Nine and Ten digit squares

It is well known that the square of 11826 ( 139854276 ) contains all the digits 1...9
and that the square of 32043 ( 1026753849 ) contains all the digits 0...9.
Others have investigated cases where the digits in the square are repeated more than once.
I have extended this investigation up to the 6th repeat of the digits. My findings are shown below.

NDComments
11826    [ A071519 ]
30384

335180136
999390432

10546200195312
31621017808182

333350001269641272
999994443856900365

10540978243301566001337
31622759033293797517068

394589436883062505110868355361		 1
1

2
2

3
3

4
4

5
5

6		 Smallest
Largest

Smallest
Largest

Smallest
Largest

Smallest
Largest

Smallest
Largest

Probably not the smallest
Where D = The number of times the 9 digits (1...9) are repeated in N squared



NDComments
32043    [ A054038 ]
99066

3164252736
9994363488

316245509988426
999944387118711

31622952459028694643
99999444387327303945

3162279417919838932896672
9999994444387345066672935

316227783585222352038673081356
> 9.9999994 x 10^29		 1
1

2
2

3
3

4
4

5
5

6
6		 Smallest
Largest

Smallest
Largest

Smallest
Largest

Smallest
Largest

Smallest
Largest

Smallest
Largest
Where D = The number of times the 10 digits (0...9) are repeated in N squared

I haven't yet found the largest example where all ten digits are repeated 6 times.
Perhaps someone else can find it and perhaps extend the table even further.

While searching for the above I came across the following interesting pair:

A = 3162455132903162 = 100011224676255433788499379856
B = 3162455165903162 = 100011226763475832394584979856

A and B differ by only two digits!

Pandigital squares

It is well known that the squares of A = 57321 and B = 60984 each contain all ten digits
and that 'A & B' combined also contains the ten digits. I wondered whether such results
could be extended such that 'A & B' contain the digits repeated twice. I very soon found
literally hundreds of solutions of which the following type is of interest:

A = 41514322532 = 17234389751248656009
B = 99860760782 = 99721715435603862084

Note that the squares of 'A' & 'B' each contain all ten digits repeated twice,
'A' contains no digit larger than 5 and 'A & B' combined contains all ten digits repeated twice.
There are many other such examples.

There are also many examples where 'A' and 'B' are pan-digital. E.g.:

A = 31754620892 = 10083559478676243921
B = 31758042692 = 10085732754998624361

Similarly the following are pan-9-digital

A = 3459186722 = 119659727638243584
B = 3519876242 = 123895287449165376

While searching for these examples I came across the following remarkable trio:

42539071862 = 1809572634_7102438596
52960318742 = 2804795361_0423951876
64320159872 = 4137082965_7023584169

Notice that the digits 0...9 are contained in each 'half' of the square
on the right hand side. There are no pan-9-digital equivalents.
[ Tom Marlow discovered only the first two squares. He submitted it to Ed Pegg's
Mathpuzzle site. Source material added 26 January 2003.]

Complete listing of the above squared nine- and pandigitals
with the higher powers as well,
up to the fifth for ninedigitals
up to the sixth for pandigitals
available at https://web.archive.org/web/20040909153834/http://blue.kakiko.com/mmrmmr/htm/eqtn11.html

Palindromes

There are many examples where N is a palindrome.

358532 = 1285437609
846482 = 7165283904
977792 = 9560732841

3819991832 = 145923375812667489
9624942692 = 926395217857844361

44025520442 = 19382464500128577936
62652256262 = 39253052144687091876
77772277772 = 60485271895340361729
92946649292 = 86390796142382575041

117248448427112 = 137471986585646734329829521
118991441998112 = 141589632687895763492435721
125672112765212 = 157934799268716582325863441
185883663885812 = 345527364996127848287193561
189171661719812 = 357859175978342281269464361
239059229509322 = 571493152135897342879668624
240623113260422 = 578994826351369112427385764
242481661842422 = 587973563298617234289114564
260568008650622 = 678956871321495791532263844
278618448168722 = 776282396599457131215864384
287203223027822 = 824856913175677163284939524

3194361316349132 = 102039442193877465886320517569
3195236263259132 = 102095347780461683147295283569
3198000600089132 = 102272078381704355869639441569
Etc.

I have not found any solutions where the square is also a palindrome
and I suspect that none exist.

Higher powers

It is natural to ask whether the above results can be extended to higher powers.
The answer is of course "yes!"

E.g.

7205585 = 194242706843325709850513196768
(digits 0...9 repeated 3 times)

In the following, the notation (N, P, D) means that the digits 1...9 (or 0...9)
are repeated 'D' times in the value of NP.

Nine digit examples:

(N, 3, 2) has 2 solutionsN = 496536, 982617
(N, 4, 2) has 1 solutionN = 24267
(N, 4, 3) has 8 solutionsN = 3374532, 3928791, 4143474, 4552878, 4714896, 4796571, 4905006, 5577408
(N, 5, 4) has 2 solutionsN = 12036828, 12343788

Ten digit examples:    [ A074205 ]

(N, 3, 2) has 138 solutionsN = 2158479, 2190762, 2205528, 2219322, ... ..., 4631793
(N, 4, 2) has 4 solutionsN = 69636, 70215, 77058, 80892
(N, 5, 3) has 7 solutionsN = 643905, 680061, 720558, 775113, 840501, 878613, 984927
(N, 6, 4) has ? solutionsN = 3470187, ... Source: OEIS
(N, 7, 4) has 2 solutionsN = 421359, 493107
(N, 8, 5) has ? solutionsN = 1472157, ... Source: OEIS
(N, 9, 5) has 1 solutionN = 320127
(N, 9, 6) has 1 solutionN = 3976581
(N, 10, 8) has ? solutionsN = 81785058, ... ..., 95927037
(N, 11, 8) has 1 solutionN = 15763347
(N, 12, 9) has 1 solutionN = 31064268
(N, 13,10) has 2 solutionsN = 44626422, 44695491
(N, 14, 12) has 2 solutionsN = 330096453, 346527657
(N, 15, 12) has 1 solutionN = 85810806

The challenge above was to make 'D' as small as possible for any particular 'P'.
I also have constructed a table of smallest and largest of any particular type
up to and including P = 15.

There are also examples where P = D in viz:

Nine digit examples:

(481514667, 3, 3) Smallest(998782725, 3, 3) Largest
(590291892, 4, 4) Smallest(998709318, 4, 4) Largest
(653813013, 5, 5) Smallest(989543343, 5, 5) Largest
(853836318, 6, 6) Smallest(897702789, 6, 6) Largest

I have not yet found any example where P = D = 7 and I suspect there are none
because it becomes increasingly unlikely that the power of any number will not
contain a zero when P is large.

Ten digit examples:

(4642110594, 3, 3) Smallest(9999257781, 3, 3) Largest
(5623720662, 4, 4) Smallest(9999112926, 4, 4) Largest
(6312942339, 5, 5) Smallest(9995722269, 5, 5) Largest
(6813614229, 6, 6) Smallest(9999409158, 6, 6) Largest
(7197035958, 7, 7) Smallest(9998033316, 7, 7) Largest
(7513755246, 8, 8) Smallest(9993870774, 8, 8) Largest
(7747685775, 9, 9) Smallest(9986053188, 9, 9) Largest
(7961085846, 10, 10) Smallest(9964052493, 10, 10) Largest
(8120306331, 11, 11) Smallest(9975246786, 11, 11) Largest
(8275283289, 12, 12) Smallest(9966918135, 12, 12) Largest
(8393900487, 13, 13) Smallest(9938689137, 13, 13) Largest
(8626922994, 14, 14) Smallest(9998781633, 14, 14) Largest
(8594070624, 15, 15) Smallest(9813743148, 15, 15) Largest

I have not checked any power larger than 15 as yet.

Pandigital powers

There are a few examples where 'N' is pandigital.

Complete listing available at https://web.archive.org/web/20040909153834/http://blue.kakiko.com/mmrmmr/htm/eqtn11.html

Nine digit examples:

(345918672, 2, 2) Smallest(976825431, 2, 2) Largest# 28
 

John Morse's list that his computer program generated for
those # 28 order-2 ninedigital squares [ April 4, 2008 ]
345918672^2 = 119659727638243584
351987624^2 = 123895287449165376
359841267^2 = 129485737436165289
394675182^2 = 155768499286733124
429715863^2 = 184655722913834769
439516278^2 = 193174558626973284
487256193^2 = 237418597616853249
527394816^2 = 278145291943673856
527498163^2 = 278254311968374569
528714396^2 = 279538912537644816
572493816^2 = 327749169358241856
592681437^2 = 351271285764384969
729564183^2 = 532263897116457489
746318529^2 = 556991346728723841
749258163^2 = 561387794822134569
754932681^2 = 569923352841847761
759142683^2 = 576297613152438489
759823641^2 = 577331965422496881
762491835^2 = 581393798441667225
783942561^2 = 614565938947238721
784196235^2 = 614963734988175225
845691372^2 = 715193896675242384
891357624^2 = 794518413862925376
914863275^2 = 836974811943725625
915786423^2 = 838664772551134929
923165487^2 = 852234516387947169
928163754^2 = 861487954239372516
976825431^2 = 954187922648335761

(516473892, 3, 3) Smallest(751396842, 3, 3) Largest# 5
(N, 4, 4) No solutions# 0
(961527834, 5, 5) only 1 solution# 1

Ten digit examples:

(3175462089, 2, 2) Smallest(9876124053, 2, 2) Largest# 534
(4680215379, 3, 3) Smallest(9863527104, 3, 3) Largest# 74
(5702631489, 4, 4) Smallest(9846032571, 4, 4) Largest# 13
(7351062489, 5, 5) Smallest(9847103256, 5, 5) Largest# 8
(7025869314, 6, 6) Smallest(9247560381, 6, 6) Largest# 6

There do not appear to be any examples for higher powers.

A curious pan-digital example is the following

9758041263 = 929154533715687684842912376

Notice that the left hand side including the index contains the digits 0...9 and that the right hand side
contains the digits 1...9 repeated 3 times. I have found no other such example for any power.

Palindromes

To date I haven't searched for palindrome solutions for cubes and higher powers
but I have no reason to believe that they do not exist. I'll investigate further when
I have a bit more time.


  Topic 4.2   [ May 18, 2005 ]
Nine and Ten digit powers
More results from Peter Kogel

Here are some more results from Peter Kogel which can be added as an addendum :

333333500000125024109149626 squared, contains the digits 1..9 repeated six times (smallest) 111111222222333349447774470014236868657845737074239129
999999944444387333120727861 squared, contains the digits 1..9 repeated six times (largest) 999999888888777752667554514316632321351744642421635321

3162277835852223520386730813562 contains digits 0..9 repeated six times (smallest) 100000011111222223236955438883649634757986945845567794798736
9999999444443873456035583500562 contains digits 0..9 repeated six times (largest) 999999888888777777633214105446041204560215564562321035203136

32541967082 = 10589_7962143580_37264 digits 0..9 contained in the centre and each digit repeated twice overall
85916740232 = 73816_8625174930_04529 ditto
89520631742 = 80139_4350712869_54276 ditto
90761483522 = 82376_4689075123_15904 ditto
96831047522 = 93762_5176382049_81504 ditto
97058431262 = 94203_3907865214_51876 ditto

43259073 = 80952_7368052419_17643 digits 0..9 contained in the centre (only cubic example)

869122976116 contains the digits 0..9 repeated sixteen times (smallest)
997090225216 contains the digits 0..9 repeated sixteen times (largest)

880038967817 contains the digits 0..9 repeated seventeen times (smallest)
974038376717 contains the digits 0..9 repeated seventeen times (largest)

998581978520 =
972018388122736146908354492278598571766247280628254566407260946047011341
594668735384194513571360871003364967097249794743843109249267940157739156
83917180391558815561723889985220630315208530426025390625

Ie. the 200 digit number contains each digit 0..9 repeated 20 times!
This is the largest such example.

" I used Yuji Kida's excellent UBASIC for all my calculations. The
program I wrote is not very elegant (I am only an amateur programmer)
and the algorithm I developed is probably far from optimal. Indeed,
from what I have learned from this project I would probably tackle it
from a completely different angle if I were ever to do it again. "


  Topic 4.1   [ December 29, 2004 ]
Solutions for ABC + DEF = GHI
Linda Rojewski

Linda Rojewski asked for all the combinations of a three digit number added
to a three digit number to equal a three digit number. You can only use digits 1-9,
and can not use any number twice. You can add to carry over a number of which
this number would not count as usage of that number.

Solution:
I (pdg) used the well known UBASIC tool and the result is listed below.
In total there are 336 solutions though not all are unique!
124 + 659 = 783 is listed as well as 659 + 124 = 783.

Question:
From this list it should be easy to extract only the distinct solutions.
How many do you count ?
Send them in and I will highlight them.

1 	124659783	 124 + 659 = 783 
2 	125739864	 125 + 739 = 864 
3 	127359486	 127 + 359 = 486 
4 	127368495	 127 + 368 = 495 
5 	128367495	 128 + 367 = 495 
6 	128439567	 128 + 439 = 567 
7 	129357486	 129 + 357 = 486 
8 	129438567	 129 + 438 = 567 
9 	129654783	 129 + 654 = 783 
10 	129735864	 129 + 735 = 864 
11 	134658792	 134 + 658 = 792 
12 	135729864	 135 + 729 = 864 
13 	138429567	 138 + 429 = 567 
14 	138654792	 138 + 654 = 792 
15 	139428567	 139 + 428 = 567 
16 	139725864	 139 + 725 = 864 
17 	142596738	 142 + 596 = 738 
18 	142695837	 142 + 695 = 837 
19 	143586729	 143 + 586 = 729 
20 	145692837	 145 + 692 = 837 
21 	146583729	 146 + 583 = 729 
22 	146592738	 146 + 592 = 738 
23 	152487639	 152 + 487 = 639 
24 	152784936	 152 + 784 = 936 
25 	154629783	 154 + 629 = 783 
26 	154638792	 154 + 638 = 792 
27 	154782936	 154 + 782 = 936 
28 	157329486	 157 + 329 = 486 
29 	157482639	 157 + 482 = 639 
30 	158634792	 158 + 634 = 792 
31 	159327486	 159 + 327 = 486 
32 	159624783	 159 + 624 = 783 
33 	162387549	 162 + 387 = 549 
34 	162783945	 162 + 783 = 945 
35 	163782945	 163 + 782 = 945 
36 	167328495	 167 + 328 = 495 
37 	167382549	 167 + 382 = 549 
38 	168327495	 168 + 327 = 495 
39 	173286459	 173 + 286 = 459 
40 	173295468	 173 + 295 = 468 
41 	175293468	 175 + 293 = 468 
42 	176283459	 176 + 283 = 459 
43 	182367549	 182 + 367 = 549 
44 	182394576	 182 + 394 = 576 
45 	182457639	 182 + 457 = 639 
46 	182493675	 182 + 493 = 675 
47 	182754936	 182 + 754 = 936 
48 	182763945	 182 + 763 = 945 
49 	183276459	 183 + 276 = 459 
50 	183492675	 183 + 492 = 675 
51 	183546729	 183 + 546 = 729 
52 	183762945	 183 + 762 = 945 
53 	184392576	 184 + 392 = 576 
54 	184752936	 184 + 752 = 936 
55 	186273459	 186 + 273 = 459 
56 	186543729	 186 + 543 = 729 
57 	187362549	 187 + 362 = 549 
58 	187452639	 187 + 452 = 639 
59 	192384576	 192 + 384 = 576 
60 	192483675	 192 + 483 = 675 
61 	192546738	 192 + 546 = 738 
62 	192645837	 192 + 645 = 837 
63 	193275468	 193 + 275 = 468 
64 	193482675	 193 + 482 = 675 
65 	194382576	 194 + 382 = 576 
66 	195273468	 195 + 273 = 468 
67 	195642837	 195 + 642 = 837 
68 	196542738	 196 + 542 = 738 
69 	214569783	 214 + 569 = 783 
70 	214659873	 214 + 659 = 873 
71 	215478693	 215 + 478 = 693 
72 	215748963	 215 + 748 = 963 
73 	216378594	 216 + 378 = 594 
74 	216738954	 216 + 738 = 954 
75 	218349567	 218 + 349 = 567 
76 	218376594	 218 + 376 = 594 
77 	218439657	 218 + 439 = 657 
78 	218475693	 218 + 475 = 693 
79 	218736954	 218 + 736 = 954 
80 	218745963	 218 + 745 = 963 
81 	219348567	 219 + 348 = 567 
82 	219438657	 219 + 438 = 657 
83 	219564783	 219 + 564 = 783 
84 	219654873	 219 + 654 = 873 
85 	234657891	 234 + 657 = 891 
86 	235746981	 235 + 746 = 981 
87 	236718954	 236 + 718 = 954 
88 	236745981	 236 + 745 = 981 
89 	237654891	 237 + 654 = 891 
90 	238419657	 238 + 419 = 657 
91 	238716954	 238 + 716 = 954 
92 	239418657	 239 + 418 = 657 
93 	241596837	 241 + 596 = 837 
94 	243576819	 243 + 576 = 819 
95 	243675918	 243 + 675 = 918 
96 	245673918	 245 + 673 = 918 
97 	245718963	 245 + 718 = 963 
98 	245736981	 245 + 736 = 981 
99 	246573819	 246 + 573 = 819 
100 	246591837	 246 + 591 = 837 
101 	246735981	 246 + 735 = 981 
102 	248319567	 248 + 319 = 567 
103 	248715963	 248 + 715 = 963 
104 	249318567	 249 + 318 = 567 
105 	251397648	 251 + 397 = 648 
106 	254619873	 254 + 619 = 873 
107 	254637891	 254 + 637 = 891 
108 	257391648	 257 + 391 = 648 
109 	257634891	 257 + 634 = 891 
110 	259614873	 259 + 614 = 873 
111 	264519783	 264 + 519 = 783 
112 	269514783	 269 + 514 = 783
 
113 	271593864	 271 + 593 = 864
114 	271683954	 271 + 683 = 954 
115 	273186459	 273 + 186 = 459 
116 	273195468	 273 + 195 = 468 
117 	273546819	 273 + 546 = 819 
118 	273591864	 273 + 591 = 864 
119 	273645918	 273 + 645 = 918 
120 	273681954	 273 + 681 = 954 
121 	275193468	 275 + 193 = 468 
122 	275418693	 275 + 418 = 693 
123 	275643918	 275 + 643 = 918 
124 	276183459	 276 + 183 = 459 
125 	276318594	 276 + 318 = 594 
126 	276543819	 276 + 543 = 819 
127 	278316594	 278 + 316 = 594 
128 	278415693	 278 + 415 = 693 
129 	281394675	 281 + 394 = 675 
130 	281673954	 281 + 673 = 954 
131 	283176459	 283 + 176 = 459 
132 	283671954	 283 + 671 = 954 
133 	284391675	 284 + 391 = 675 
134 	286173459	 286 + 173 = 459 
135 	291357648	 291 + 357 = 648 
136 	291384675	 291 + 384 = 675 
137 	291546837	 291 + 546 = 837 
138 	291573864	 291 + 573 = 864 
139 	293175468	 293 + 175 = 468 
140 	293571864	 293 + 571 = 864 
141 	294381675	 294 + 381 = 675 
142 	295173468	 295 + 173 = 468 
143 	296541837	 296 + 541 = 837 
144 	297351648	 297 + 351 = 648 
145 	314658972	 314 + 658 = 972 
146 	316278594	 316 + 278 = 594 
147 	317529846	 317 + 529 = 846 
148 	317628945	 317 + 628 = 945 
149 	318249567	 318 + 249 = 567 
150 	318276594	 318 + 276 = 594 
151 	318627945	 318 + 627 = 945 
152 	318654972	 318 + 654 = 972 
153 	319248567	 319 + 248 = 567 
154 	319527846	 319 + 527 = 846 
155 	324567891	 324 + 567 = 891 
156 	324657981	 324 + 657 = 981 
157 	327159486	 327 + 159 = 486 
158 	327168495	 327 + 168 = 495 
159 	327519846	 327 + 519 = 846 
160 	327564891	 327 + 564 = 891 
161 	327618945	 327 + 618 = 945 
162 	327654981	 327 + 654 = 981 
163 	328167495	 328 + 167 = 495 
164 	328617945	 328 + 617 = 945 
165 	329157486	 329 + 157 = 486 
166 	329517846	 329 + 517 = 846 
167 	341586927	 341 + 586 = 927 
168 	342576918	 342 + 576 = 918 
169 	346572918	 346 + 572 = 918 
170 	346581927	 346 + 581 = 927 
171 	348219567	 348 + 219 = 567 
172 	349218567	 349 + 218 = 567 
173 	351297648	 351 + 297 = 648 
174 	352467819	 352 + 467 = 819 
175 	354618972	 354 + 618 = 972 
176 	354627981	 354 + 627 = 981 
177 	357129486	 357 + 129 = 486 
178 	357291648	 357 + 291 = 648 
179 	357462819	 357 + 462 = 819 
180 	357624981	 357 + 624 = 981 
181 	358614972	 358 + 614 = 972 
182 	359127486	 359 + 127 = 486 
183 	362187549	 362 + 187 = 549 
184 	362457819	 362 + 457 = 819 
185 	364527891	 364 + 527 = 891 
186 	367128495	 367 + 128 = 495 
187 	367182549	 367 + 182 = 549 
188 	367452819	 367 + 452 = 819 
189 	367524891	 367 + 524 = 891 
190 	368127495	 368 + 127 = 495 
191 	372546918	 372 + 546 = 918 
192 	376218594	 376 + 218 = 594 
193 	376542918	 376 + 542 = 918 
194 	378216594	 378 + 216 = 594 
195 	381294675	 381 + 294 = 675 
196 	381546927	 381 + 546 = 927 
197 	382167549	 382 + 167 = 549 
198 	382194576	 382 + 194 = 576 
199 	384192576	 384 + 192 = 576 
200 	384291675	 384 + 291 = 675 
201 	386541927	 386 + 541 = 927 
202 	387162549	 387 + 162 = 549 
203 	391257648	 391 + 257 = 648 
204 	391284675	 391 + 284 = 675 
205 	392184576	 392 + 184 = 576 
206 	394182576	 394 + 182 = 576 
207 	394281675	 394 + 281 = 675 
208 	397251648	 397 + 251 = 648 
209 	415278693	 415 + 278 = 693 
210 	418239657	 418 + 239 = 657 
211 	418275693	 418 + 275 = 693 
212 	419238657	 419 + 238 = 657 
213 	428139567	 428 + 139 = 567 
214 	429138567	 429 + 138 = 567 
215 	438129567	 438 + 129 = 567 
216 	438219657	 438 + 219 = 657 
217 	439128567	 439 + 128 = 567 
218 	439218657	 439 + 218 = 657 
219 	452187639	 452 + 187 = 639 
220 	452367819	 452 + 367 = 819 
221 	457182639	 457 + 182 = 639 
222 	457362819	 457 + 362 = 819 
223 	462357819	 462 + 357 = 819 
224 	467352819	 467 + 352 = 819
 
225 	475218693	 475 + 218 = 693 
226 	478215693	 478 + 215 = 693 
227 	482157639	 482 + 157 = 639 
228 	482193675	 482 + 193 = 675 
229 	483192675	 483 + 192 = 675 
230 	487152639	 487 + 152 = 639 
231 	492183675	 492 + 183 = 675 
232 	493182675	 493 + 182 = 675 
233 	514269783	 514 + 269 = 783 
234 	517329846	 517 + 329 = 846 
235 	519264783	 519 + 264 = 783 
236 	519327846	 519 + 327 = 846 
237 	524367891	 524 + 367 = 891 
238 	527319846	 527 + 319 = 846 
239 	527364891	 527 + 364 = 891 
240 	529317846	 529 + 317 = 846 
241 	541296837	 541 + 296 = 837 
242 	541386927	 541 + 386 = 927 
243 	542196738	 542 + 196 = 738 
244 	542376918	 542 + 376 = 918 
245 	543186729	 543 + 186 = 729 
246 	543276819	 543 + 276 = 819 
247 	546183729	 546 + 183 = 729 
248 	546192738	 546 + 192 = 738 
249 	546273819	 546 + 273 = 819 
250 	546291837	 546 + 291 = 837 
251 	546372918	 546 + 372 = 918 
252 	546381927	 546 + 381 = 927 
253 	564219783	 564 + 219 = 783 
254 	564327891	 564 + 327 = 891 
255 	567324891	 567 + 324 = 891 
256 	569214783	 569 + 214 = 783 
257 	571293864	 571 + 293 = 864 
258 	572346918	 572 + 346 = 918 
259 	573246819	 573 + 246 = 819 
260 	573291864	 573 + 291 = 864 
261 	576243819	 576 + 243 = 819 
262 	576342918	 576 + 342 = 918 
263 	581346927	 581 + 346 = 927 
264 	583146729	 583 + 146 = 729 
265 	586143729	 586 + 143 = 729 
266 	586341927	 586 + 341 = 927 
267 	591246837	 591 + 246 = 837 
268 	591273864	 591 + 273 = 864 
269 	592146738	 592 + 146 = 738 
270 	593271864	 593 + 271 = 864 
271 	596142738	 596 + 142 = 738 
272 	596241837	 596 + 241 = 837 
273 	614259873	 614 + 259 = 873 
274 	614358972	 614 + 358 = 972 
275 	617328945	 617 + 328 = 945 
276 	618327945	 618 + 327 = 945 
277 	618354972	 618 + 354 = 972 
278 	619254873	 619 + 254 = 873 
279 	624159783	 624 + 159 = 783 
280 	624357981	 624 + 357 = 981 
281 	627318945	 627 + 318 = 945 
282 	627354981	 627 + 354 = 981 
283 	628317945	 628 + 317 = 945 
284 	629154783	 629 + 154 = 783 
285 	634158792	 634 + 158 = 792 
286 	634257891	 634 + 257 = 891 
287 	637254891	 637 + 254 = 891 
288 	638154792	 638 + 154 = 792 
289 	642195837	 642 + 195 = 837 
290 	643275918	 643 + 275 = 918 
291 	645192837	 645 + 192 = 837 
292 	645273918	 645 + 273 = 918 
293 	654129783	 654 + 129 = 783 
294 	654138792	 654 + 138 = 792 
295 	654219873	 654 + 219 = 873 
296 	654237891	 654 + 237 = 891 
297 	654318972	 654 + 318 = 972 
298 	654327981	 654 + 327 = 981 
299 	657234891	 657 + 234 = 891 
300 	657324981	 657 + 324 = 981 
301 	658134792	 658 + 134 = 792 
302 	658314972	 658 + 314 = 972 
303 	659124783	 659 + 124 = 783 
304 	659214873	 659 + 214 = 873 
305 	671283954	 671 + 283 = 954 
306 	673245918	 673 + 245 = 918 
307 	673281954	 673 + 281 = 954 
308 	675243918	 675 + 243 = 918 
309 	681273954	 681 + 273 = 954 
310 	683271954	 683 + 271 = 954 
311 	692145837	 692 + 145 = 837 
312 	695142837	 695 + 142 = 837 
313 	715248963	 715 + 248 = 963 
314 	716238954	 716 + 238 = 954 
315 	718236954	 718 + 236 = 954 
316 	718245963	 718 + 245 = 963 
317 	725139864	 725 + 139 = 864 
318 	729135864	 729 + 135 = 864 
319 	735129864	 735 + 129 = 864 
320 	735246981	 735 + 246 = 981 
321 	736218954	 736 + 218 = 954 
322 	736245981	 736 + 245 = 981 
323 	738216954	 738 + 216 = 954 
324 	739125864	 739 + 125 = 864 
325 	745218963	 745 + 218 = 963 
326 	745236981	 745 + 236 = 981 
327 	746235981	 746 + 235 = 981 
328 	748215963	 748 + 215 = 963 
329 	752184936	 752 + 184 = 936 
330 	754182936	 754 + 182 = 936 
331 	762183945	 762 + 183 = 945 
332 	763182945	 763 + 182 = 945 
333 	782154936	 782 + 154 = 936 
334 	782163945	 782 + 163 = 945 
335 	783162945	 783 + 162 = 945 
336 	784152936	 784 + 152 = 936


For reference goals and easy searching I list here all the nine- & pandigitals implicitly displayed in these topics.

Topic 4.7 →
Case 9-9 → 329586147, 238756941, 234681597, 351728649, 2356948171, 234586917, 317582649, 235469781, 238756941, 361958427, 234956871, 389452671, 235694817, 348795261, 236475981, 237185469, 361278459, 325168947, 372548961, 231487569, 361942857, 372851469, 342615897, 346758129, 234651987, 356824791, 357142869
Case 10-10 → 3716245809, 3285740169, 2319680547, 2360874159, 2360874591, 3526840971, 3540196827, 3528176409, 3281950647, 3580124697, 2374598061, 2376054189, 2376094581, 2351706849, 3592608147, 3510268497, 3580126947, 2358016947, 3672418509, 2317608459, 3286159407, 2387415609, 2358741609, 2387456091, 2387459061, 3604729851, 3725806419, 3725840961, 3512069487, 2390587461, 2357649801, 2394085671, 2347106589, 3547806129, 2357684109, 2356401987, 2348569701, 2316509487, 2371468059, 3728640519, 3540896217, 2361758049, 2354190687, 2354816907, 2351469087, 2364187509, 2374165809, 2318906457, 3546218097, 2314859067, 2354860971, 2341578069, 3487562901, 2345809167, 2357140689, 3281509647, 3509182467, 3416825097, 3296475081, 3741052689, 3614725089, 2349150687, 3561429087, 3520714689, 3752098641, 3745018269, 3745268901, 2358016947, 3794085621, 2354071869, 3746802159, 3294780651, 3508721649, 3748562109, 2314568097, 3570821649, 3751042689, 3621758049, 3612095487, 2310654879, 3508176249, 2348570169, 2354961087, 2349805761, 2371468059, 3596820147, 3472869051, 3581064729, 3516420897, 2356980417, 2354671809, 2370465981, 2370498651, 3720156489, 3586492017, 2374618059, 3589620417, 2374165809, 2356879401, 2389641057, 2357068941, 3895164207, 2357486901, 3269580471, 3289754601, 2354071869, 2357804619, 2358469017, 2358470169, 3520817649, 2341708569, 3296105487, 2341578069, 3281647509, 3618954027, 2391865047, 2346081579, 2354189607, 2310568479, 2349150687, 2354980671, 2318706459, 2375106849, 2340168759, 2358046197, 2358190467, 2317405869, 3976852401, 3526840971, 3859264071, 2356847019, 2356879401, 3297864501, 2386190547, 3409562781, 2357690481, 3546728109, 2314650897, 3415809627, 3510746829, 2390546817, 2315096847, 3467518209, 2345706891, 2347986501, 2351406897, 2314098657, 2351706849, 2364578901, 2365109487, 2365170849, 2354961087, 2349680157, 3716254089, 2350861749, 2345698701, 2370415869, 2370465981, 2370569481, 2359746081, 3560219487, 3512069487, 3809124567, 3560479281, 2357186049, 2359864107, 2378510469, 2346157089, 3172085469, 3512804769, 3540816729, 2310854769, 3615708429, 2365491087, 2314785609, 3542680971, 2357849061, 3862941507, 3751642089, 3619584027, 2316950487, 2316750849, 3572604981, 2360584971
Case 10-9 → 231784659, 239684517, 382715649, 231658749, 237564981, 351842769, 235897641, 236145879, 239516847, 329586741, 235641897, 234961587, 352167849, 371256489, 234615987, 239856471, 235948761, 235698471, 354217869, 354278619, 375418629, 235194687, 354196827, 236759481, 351726489, 235968147, 364715289, 354617829, 375624891, 369145827, 356428197, 374618529, 234156897, 235978641, 239516847, 376254891, 234761859, 238764519, 352614987, 236479851, 357416829, 234615987, 396745821, 236418759, 357126849, 359274861, 324167589, 354127689, 239654781, 235187469, 367845921, 378215469, 239857641, 354267819, 234619587, 368579241, 326598147, 325784691, 238764519, 236914587, 236159487, 235748619, 235496817, 235649871, 235164897, 356287419, 235764891, 239674851, 235476189, 357946821, 236914587, 358124679, 235964871, 236485719, 237564981, 354762189
Case 9-10 → 2310698547, 2310846597, 2310874659, 2316584097, 2317408659, 3541206897, 2310698547, 3510842697, 3127465809, 2358016947, 2340658719, 2314687509, 3518620947, 2359860417, 3714528069, 3472165089, 3257416089, 2318046597, 2354618097

Topic 4.5 →
Top → 213458796, 253817649, 294317586, 539246718, 539462718, 273568149, 273586149, 917264358
P=2 → 159624837, 163529487, 187524693, 236719485, 243618975, 253817649, 278415369, 294317586, 349512768, 351628479, 365412897, 384629175, 386425179, 391528467, 398426715, 419725638, 435916278, 439527186, 453612987, 469821357, 485721396, 489621753, 496517382, 496815237, 536714928, 537612984, 537618429, 543617289, 546913728, 549618237, 561327948, 567914238, 569721384, 576321948, 596418273, 597621483, 618925374, 619823547, 634521987, 645319287, 645917328, 647123589, 647129538, 652813749, 654927831, 681324597, 683129745, 694513782, 697514823, 716425983, 735624189, 735928146, 743129658, 745823619, 765913248, 765913428, 782419356, 786321495, 786923514, 795316824, 825913476, 829514763, 834917562, 835217469, 851729643, 874516392, 879312546, 879621345, 879623541, 893415267, 897312546, 897625413, 915627483, 916823475, 962718543, 968724513, 973524861, 974126358
P=3 → 123465897, 124389576, 124635789, 124639875, 126593784, 128634759, 129375468, 129365847, 132479865, 135297684, 136582749, 137286954, 138259746, 138264795, 139576824, 142396857, 145297863, 145296873, 145693728, 146397825, 147265983, 149258637, 153469728, 156492738, 159423768, 162354789, 165324789, 165234978, 167532894, 172348596, 175629843, 176549832, 178426593, 182379564, 184527936, 186395742, 189246537, 192548763, 192356847, 193468572, 194285736, 194376825, 194627835, 196273458, 196342785, 197364825, 198243675, 213467589, 213578649, 215378496, 216397485, 216387495, 219438567, 219436587, 231456789, 234619857, 237654819, 246539718, 249381675, 251486739, 253419768, 254391768, 258314697, 259641837, 261457938, 267384951, 269537841, 271398546, 271458639, 274591863, 278351496, 279413856, 312479658, 317489526, 318547692, 321498576, 321564897, 328519674, 342596871, 351468792, 362459718, 372519864, 374526918, 378512649, 381469572, 386519724, 394561728, 397458621, 398415672, 418693725, 429576831, 429671835, 462539718, 483597621, 487521693, 489613725, 493581627, 493512786, 514639782, 574639812, 591624738
P=4 → 246978135, 273568149, 273586149, 485796123, 647285139
P=5 → 917264358


Contributions

Linda Rojewski (email) - go to topic

Peter Kogel (email) - go to topic - go to topic addendum - go to more ninedigital powers

John Morse (email) - go to topic

[up TOP OF PAGE]

( © All rights reserved ) - Last modified : November 19, 2025.
Patrick De Geest - Belgium flag - Short Bio - Some Pictures
E-mail address : pdg@worldofnumbers.com