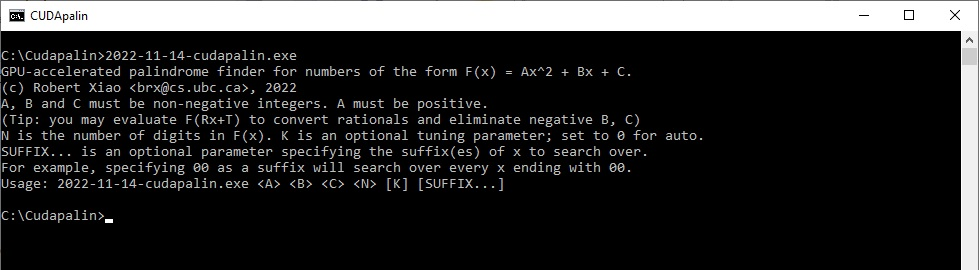
It is best to leave the [K] parameter set to zero. This is intended for the specialists. Now let us perform our first search for palindromic squares of length [N] being the number of digits of the square for all possible base enddigits from 0 to 9. That is why the [SUFFIX...] parameter is left out. And here is the output :
C:\Cudapalin>2022-11-14-cudapalin.exe 1 0 0 7 0
Finding length-7 palindromes of the form F(x) = x^2 (using K = 2)
Processing suffix 1
1001 1002001
1111 1234321
Finished suffix 1 in 0.001315s
Processing suffix 2
2002 4008004
Finished suffix 2 in 0.000528s
Processing suffix 3
Finished suffix 3 in 0.000320s
Processing suffix 4
Finished suffix 4 in 0.000337s
Processing suffix 5
2285 5221225
Finished suffix 5 in 0.000480s
Processing suffix 6
2636 6948496
Finished suffix 6 in 0.000445s
Processing suffix 7
Finished suffix 7 in 0.000334s
Processing suffix 8
Finished suffix 8 in 0.000423s
Processing suffix 9
Finished suffix 9 in 0.000345s
Finished finding length-7 palindromes of the form F(x) = x^2 (K = 2) in 0.005238s
|
So the program found 5 solutions of square length-7 in almost no time! Note that the first three are non-sporadic solutions. Redo the search now for length-48 palindromes :
C:\CUDApalin>2022-11-14-cudapalin 1 0 0 48 0
Finding length-48 palindromes of the form F(x) = x^2 (using K = 12)
Processing suffix 1
Finished suffix 1 in 7.087145s
Processing suffix 2
Finished suffix 2 in 4.446963s
Processing suffix 3
Finished suffix 3 in 3.420169s
Processing suffix 4
831775153121251039203514 691849905349880612384525525483216088943509948196
Finished suffix 4 in 3.858238s
Processing suffix 5
722956456358957313434535 522666037791100950480675576084059001197730666225
Finished suffix 5 in 4.144074s
Processing suffix 6
Finished suffix 6 in 3.864197s
Processing suffix 7
Finished suffix 7 in 3.432827s
Processing suffix 8
Finished suffix 8 in 4.465314s
Processing suffix 9
Finished suffix 9 in 7.117333s
Finished finding length-48 palindromes of the form F(x) = x^2 (K = 12) in 41.837423s
|
My fast computer needed almost 42 seconds to find these two even length 48-digit palindromic squares. But the timings grow exponentially with larger and larger lengths. Note also that the palindromic squares are not necessarily sorted in ascending order. It is the base with its rightmost digit(s) that makes out the order.
Here are the timings for our length-67 palindromic square with suffix 63. Suffix 63 was scanned in 21118.412571s (a little less than 6 hours). The search was first split up into a hundred parts from suffix 00 up to 99. Suffix 63 came out with the current record holder.
C:\CUDApalin>2022-11-14-cudapalin 1 0 0 67 0 63
Finding length-67 palindromes of the form F(x) = x^2 (using K = 17)
Processing suffix 63
3109885844380152888763910885950363 9671389965076056510789702463424611164243642079870156506705699831769
Finished suffix 63 in 21118.412407s
Finished finding length-67 palindromes of the form F(x) = x^2 (K = 17) in 21118.412571s
|
The timings for the suffixes might differ substantially. For instance for length-67 and suffix 01 my system needed 40463,205740s which is almost 11 hours and 15 min (double of suffix 63).
For slower pc's these timings might become days instead of hours. Hence the need for splitting the search up into more and more suffixes. Fixing already three last digits results in thousand subdivisions but with the advantage that a scan will finish in a reasonable amount of time. And that is were the distributed project comes in handy.
Some regions will raise an error when a search is started with some suffixes. With squares this is the case with suffix 0 (like 90 or 150).
C:\Cudapalin>2022-11-14-cudapalin.exe 1 0 0 7 0 90
Warning: F(x) ends with 0 for suffix 90 - results will not be valid palindromes!
Finding length-7 palindromes of the form F(x) = x^2 (using K = 2)
Processing suffix 90
Finished suffix 90 in 0.001006s
Finished finding length-7 palindromes of the form F(x) = x^2 (K = 2) in 0.001044s
|
If F(x) ends with a zero, then conventionally we will not consider them to be palindromes at all. Cudapalin checks for this condition, and normally if you don't specify any suffixes (letting the program search over all possible x values) it will skip those x values entirely. If you specify suffixes, cudapalin assumes you wanted to search for those palindromes so it prints a warning and continues.
To prevent loss of data after running cudapalin for a while one has to store the data somewhere safe from power outage or Microsoft forced OS updates or inadvertent app-closings. The usual way to do this is by storing the output in a logfile using a redirection. This has the disadvantage that the date isn't visible on screen anymore. To work around this problem we can use PowerShell for Windows (if not installed you can use this link https://github.com/PowerShell/PowerShell/releases). Then initiate 'PowerShell' from the Start Button and launch the version installed on your system. Enter the following example on the command line :
cmd /c "C:\CUDApalin\2022-11-14-cudapalin.exe 1 0 0 48 0 2>&1" | tee "C:\CUDApalin\outputcp.txt" -append
As always, once you get this gobbledygook right once, it's smooth sailing. Next is a screencopy of what I used for the last suffix 99 for length-67 squares :
|