|
[ May 16, 2021 ]
Investigating prime multidigit subsequences in the list of
9! ninedigital numbers and a programming challenge following it
Alexandru Dan Petrescu (email)
We obtain for every ninedigital number 35 numbers
having 2, 3, 4, 5, 6, 7 and respectively 8 digits.
If the minimum number of primes is 1, then we get 5251 ninedigital numbers
the largest being 987651342 (13 being the only prime).
The maximum number of primes turns out to be 16
corresponding for only one ninedigital number, namely 856342179.
Illustrating with the first ninedigital 123456789.
| 8 digits | 12345678, 23456789 |
| 7 digits | 1234567, 2345678, 3456789 |
| 6 digits | 123456, 234567, 345678, 456789 |
| 5 digits | 12345, 23456, 34567, 45678, 56789 |
| 4 digits | 1234, 2345, 3456, 4567, 5678, 6789 |
| 3 digits | 123, 234, 345, 456, 567, 678, 789 |
| 2 digits | 12, 23, 34, 45, 56, 67, 78, 89 |
| 1 digit | these are excluded |
In all 35 numbers, from which 5 are prime (numbers in blue highlight)
What about the other ninedigitals ?
That will be the intent of the next challenge.
Here we ask the reader to program in code of his choice
(Pari/gp, Mathematica, C++, Ubasic, Python, ...)
so we get more statistical information around this topic.
So let me start with Alexandru Dan Petrescu's own code using Pari/gp.
nm=vector(16);for(n=1,9!,d=numtoperm(9, n+9!-1);a=sum(i=1, #d, d[i]*10^(#d-i));\
dd=digits(a);sp=0;\
for(k=1,8,b=fromdigits([dd[k],dd[k+1]]);if(isprime(b)==1,sp++));\
for(k=1,7,b=fromdigits([dd[k],dd[k+1],dd[k+2]]);if(isprime(b)==1,sp++));\
for(k=1,6,b=fromdigits([dd[k],dd[k+1],dd[k+2],dd[k+3]]);if(isprime(b)==1,sp++));\
for(k=1,5,b=fromdigits([dd[k],dd[k+1],dd[k+2],dd[k+3],dd[k+4]]);if(isprime(b)==1,sp++));\
for(k=1,4,b=fromdigits([dd[k],dd[k+1],dd[k+2],dd[k+3],dd[k+4],dd[k+5]]);if(isprime(b)==1,sp++));\
for(k=1,3,b=fromdigits([dd[k],dd[k+1],dd[k+2],dd[k+3],dd[k+4],dd[k+5],dd[k+6]]);if(isprime(b)==1,sp++));\
for(k=1,2,b=fromdigits([dd[k],dd[k+1],dd[k+2],dd[k+3],dd[k+4],dd[k+5],dd[k+6],dd[k+7]]);\
if(isprime(b)==1,sp++));if(sp>0,nm[sp]++));for(i=1,16,write("e:/pari/wn13.txt",i,",",nm[i]))
The output becomes
0,687
1,5251
2,20015
3,41529
4,62138
5,69864
6,61983
7,46074
8,29226
9,15452
10,7023
11,2546
12,856
13,186
14,45
15,4
16,1
So the above example of ninedigital 123456789 with 5 primes as subsequences
is only one solution amidst 69864 other ninedigitals.
There is also one unique solution with 16 primes namely 856342179 !
The following code shows those 16 primes. It's by me Patrick De Geest using Ubasic.
Ubasic is a bit outdated but from time to time
I still use it for nostalgic reasons.
1000 dim Sp(35)
1010 N=cutspc(str(856342179))
1020 Sp(0)=N
1030 Cnt=0
1040 ' 8 digit subsequences * 2
1050 Sn1=val(left(N,8)):if prmdiv(Sn1)=Sn1 then Cnt+=1:Sp(Cnt)=Sn1
1060 Sn2=val(right(N,8)):if prmdiv(Sn2)=Sn2 then Cnt+=1:Sp(Cnt)=Sn2
1070 ' 7 digit subsequences * 3
1080 Sn3=val(left(N,7)):if prmdiv(Sn3)=Sn3 then Cnt+=1:Sp(Cnt)=Sn3
1090 Sn4=val(mid(N,2,7)):if prmdiv(Sn4)=Sn4 then Cnt+=1:Sp(Cnt)=Sn4
1100 Sn5=val(right(N,7)):if prmdiv(Sn5)=Sn5 then Cnt+=1:Sp(Cnt)=Sn5
1110 ' 6 digit subsequences * 4
1120 Sn6=val(left(N,6)):if prmdiv(Sn6)=Sn6 then Cnt+=1:Sp(Cnt)=Sn6
1130 Sn7=val(mid(N,2,6)):if prmdiv(Sn7)=Sn7 then Cnt+=1:Sp(Cnt)=Sn7
1140 Sn8=val(mid(N,3,6)):if prmdiv(Sn8)=Sn8 then Cnt+=1:Sp(Cnt)=Sn8
1150 Sn9=val(right(N,6)):if prmdiv(Sn9)=Sn9 then Cnt+=1:Sp(Cnt)=Sn9
1160 ' 5 digit subsequences * 5
1170 Sn10=val(left(N,5)):if prmdiv(Sn10)=Sn10 then Cnt+=1:Sp(Cnt)=Sn10
1180 Sn11=val(mid(N,2,5)):if prmdiv(Sn11)=Sn11 then Cnt+=1:Sp(Cnt)=Sn11
1190 Sn12=val(mid(N,3,5)):if prmdiv(Sn12)=Sn12 then Cnt+=1:Sp(Cnt)=Sn12
1200 Sn13=val(mid(N,4,5)):if prmdiv(Sn13)=Sn13 then Cnt+=1:Sp(Cnt)=Sn13
1210 Sn14=val(right(N,5)):if prmdiv(Sn14)=Sn14 then Cnt+=1:Sp(Cnt)=Sn14
1220 ' 4 digit subsequences * 6
1230 Sn15=val(left(N,4)):if prmdiv(Sn15)=Sn15 then Cnt+=1:Sp(Cnt)=Sn15
1240 Sn16=val(mid(N,2,4)):if prmdiv(Sn16)=Sn16 then Cnt+=1:Sp(Cnt)=Sn16
1250 Sn17=val(mid(N,3,4)):if prmdiv(Sn17)=Sn17 then Cnt+=1:Sp(Cnt)=Sn17
1260 Sn18=val(mid(N,4,4)):if prmdiv(Sn18)=Sn18 then Cnt+=1:Sp(Cnt)=Sn18
1270 Sn19=val(mid(N,5,4)):if prmdiv(Sn19)=Sn19 then Cnt+=1:Sp(Cnt)=Sn19
1280 Sn20=val(right(N,4)):if prmdiv(Sn20)=Sn20 then Cnt+=1:Sp(Cnt)=Sn20
1290 ' 3 digit subsequences * 7
1300 Sn21=val(left(N,3)):if prmdiv(Sn21)=Sn21 then Cnt+=1:Sp(Cnt)=Sn21
1310 Sn22=val(mid(N,2,3)):if prmdiv(Sn22)=Sn22 then Cnt+=1:Sp(Cnt)=Sn22
1320 Sn23=val(mid(N,3,3)):if prmdiv(Sn23)=Sn23 then Cnt+=1:Sp(Cnt)=Sn23
1330 Sn24=val(mid(N,4,3)):if prmdiv(Sn24)=Sn24 then Cnt+=1:Sp(Cnt)=Sn24
1340 Sn25=val(mid(N,5,3)):if prmdiv(Sn25)=Sn25 then Cnt+=1:Sp(Cnt)=Sn25
1350 Sn26=val(mid(N,6,3)):if prmdiv(Sn26)=Sn26 then Cnt+=1:Sp(Cnt)=Sn26
1360 Sn27=val(right(N,3)):if prmdiv(Sn27)=Sn27 then Cnt+=1:Sp(Cnt)=Sn27
1370 ' 2 digit subsequences * 8
1380 Sn28=val(left(N,2)):if prmdiv(Sn28)=Sn28 then Cnt+=1:Sp(Cnt)=Sn28
1390 Sn29=val(mid(N,2,2)):if prmdiv(Sn29)=Sn29 then Cnt+=1:Sp(Cnt)=Sn29
1400 Sn30=val(mid(N,3,2)):if prmdiv(Sn30)=Sn30 then Cnt+=1:Sp(Cnt)=Sn30
1410 Sn31=val(mid(N,4,2)):if prmdiv(Sn31)=Sn31 then Cnt+=1:Sp(Cnt)=Sn31
1420 Sn32=val(mid(N,5,2)):if prmdiv(Sn32)=Sn32 then Cnt+=1:Sp(Cnt)=Sn32
1430 Sn33=val(mid(N,6,2)):if prmdiv(Sn33)=Sn33 then Cnt+=1:Sp(Cnt)=Sn33
1440 Sn34=val(mid(N,7,2)):if prmdiv(Sn34)=Sn34 then Cnt+=1:Sp(Cnt)=Sn34
1450 Sn35=val(right(N,2)):if prmdiv(Sn35)=Sn35 then Cnt+=1:Sp(Cnt)=Sn35
1460 color 10:print Sp(0);" ";:color 15
1470 for I=1 to Cnt
1480 print Sp(I);
1490 next I
1500 color 14:print "[ #";Cnt;"primes ]":color 15
The output becomes
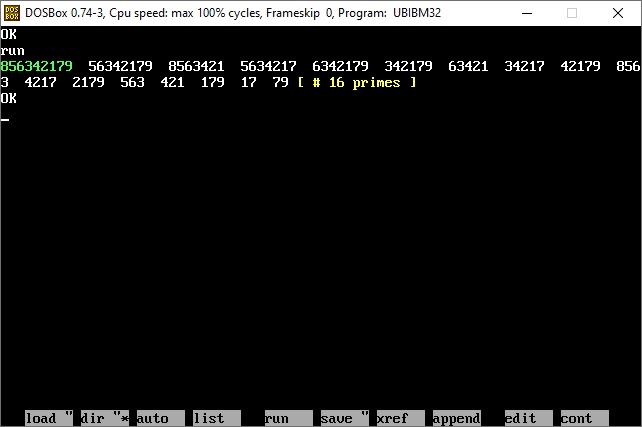
|

![]() TOP OF PAGE]
TOP OF PAGE]