[ October 12, 2001 ]
Four in a row.... Semiprimes !

I always preserved a place for semiprimes in my heart.
Semiprimes are in fact composites with exactly two prime factors,
(these are sometimes called 2-almost primes)
the next best thing to the primes themselves.

This puzzle resulted from a small investigation into the matter
for Neil Sloane's On-line Encyclopedia of Integer Sequences.
(Sequences A064899 to A064911)
In order to sample 4 terms for submitting a new sequence (the
required minimum) I need(ed) to discover four consecutive semiprimes.

The first three solutions 4, 9 and 33 were rather easy to find.
The fourth one however eluded me.

n	n consecutive semiprimes
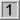	4 = 2 * 2
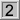	9 = 3 * 3 10 = 2 * 5
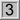	33 = 3 * 11 34 = 2 * 17 35 = 5 * 7
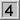	unknown impossible ?

[ October 13, 2001 ]
Very soon a reply came in from Robert G. Wilson v

There is no number for four consecutive semiprimes !

Proof
Given any 4 consecutive numbers, two of them are divisible by 2,
at least one of them is divisible by 3, and one of them is divisible by 4.
For any integer, 4m, will have at least three prime factors, 2, 2, and m.
Notice the example of 9 as being = to 3 * 3 and is defined as a semiprime.
QED.

Collecting beautiful semiprimes

[ August 24, 2002 ]
Jean Claude Rosa , while studying palindromes equal to the sum of
the squares of two consecutive integers, met these two (amongst others)
See my page sumsquare.htm (two squares - index 22)
8032814139² + 8032814140² =
129052205999502250921 =
2180006221 * 59198090701
and (two squares - index 30)
1258837943717² + 1258837943718² =
3169345937085807395439613 =
14845657 * 213486404615559109

I (pdg) myself found the following dd. [ September 1, 2002 ]
The concatenation of all the palindromes from 1 up to 11 is semiprime.
12345678911 =
3643 * 3388877

And from WONplate 48 I remembered this nice one:
The concatenation of the first 7 natural numbers is semiprime.
Moreover the two factors combined forms very
unexpectedly a palindrome !
1234567 =
127 * 9721 =
1279721

A108505 The number of palindromic semiprimes less than 10^n. - Robert G. Wilson v