\(177\mathbf{\color{blue}{\;=\;}}27+29+29+30+31+32\mathbf{\color{blue}{\;=\;}}58+59+60\mathbf{\color{blue}{\;=\;}}88+89\) (som van opeenvolgende gehele getallen)

\(177\mathbf{\color{blue}{\;=\;}}57+59+61\) (som van opeenvolgende onpare getallen)

\(177=((0;2;2;13)\,(0;7;8;8)\,(1;4;4;12)\,(2;2;5;12)\,(2;3;8;10)\,(2;4;6;11)\,(4;4;8;9)\,(4;5;6;10))\lower2pt{\Large{\color{teal}{➋}}}\to\{\#8\}\)

\(177=((0;0;0;1;2;2;2;3;5)\,(0;2;2;2;2;3;3;3;4)\,(1;2;2;2;2;2;2;4;4))\lower2pt{\Large{\color{teal}{➌}}}\to\{\#3\}\)

\(177\mathbf{\color{blue}{\;=\;}}2^3+5^2+12^2\mathbf{\color{blue}{\;=\;}}2^5+2^6+3^4\)

\(177\mathbf{\color{blue}{\;=\;}}2^3+13^2\mathbf{\color{blue}{\;=\;}}\bbox[peachpuff,3px]{2^7+7^2}\mathbf{\color{blue}{\;=\;}}31^2-28^2\mathbf{\color{blue}{\;=\;}}\bbox[2px,border:1px brown dashed]{89^2-88^2}\)

\(177\mathbf{\color{blue}{\;=\;}}\)(som van drie derdemachten)

\(\qquad~~~~5\) oplossingen bekend

\(\qquad~~~~\)References Sum of Three Cubes

\(\qquad~~~~\bbox[3px,border:1px solid]{2^3+(-7)^3+8^3}\mathbf{\color{blue}{\;=\;}}\)

\(\qquad~~~~\bbox[3px,border:1px solid]{(-160)^3+(-1168)^3+1169^3}\mathbf{\color{blue}{\;=\;}}\)

\(\qquad~~~~\bbox[3px,border:1px solid]{132113^3+813428^3+(-814588)^3}\mathbf{\color{blue}{\;=\;}}\)

\(\qquad~~~~\bbox[3px,border:1px solid]{1081968566^3+1411480634^3+(-1597740847)^3}\mathbf{\color{blue}{\;=\;}}\)

\(\qquad~~~~\bbox[3px,border:1px solid]{40073698039754^3+85300866522260^3+(-88152618881383)^3}\mathbf{\color{blue}{\;=\;}}\)

\(177\mathbf{\color{blue}{\;=\;}}\)(som van vijf vijfdemachten)

\(\qquad~~~~\bbox[3px,border:1px blue solid]{(-1)^5+(-1)^5+(-2)^5+(-2)^5+3^5}\)

\(\qquad~~~~\bbox[3px,border:1px blue solid]{(-1)^5+4^5+(-7)^5+(-7)^5+8^5}\)

\(\qquad~~~~\bbox[3px,border:1px blue solid]{(-2)^5+12^5+(-14)^5+(-15)^5+16^5}\)

\(\qquad~~~~\bbox[3px,border:1px blue solid]{(-2)^5+5^5+(-39)^5+(-48)^5+51^5}\)

\(\qquad~~~~\bbox[3px,border:1px blue solid]{(-120)^5+291^5+296^5+337^5+(-387)^5}\)

\(177^3=5545233=((55+4+5-2-3)*3)^3\)

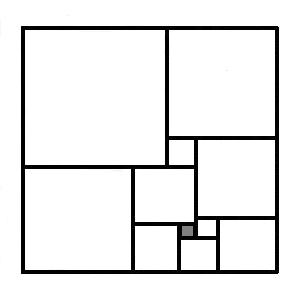
Een rechthoek van \(176\) bij \(177\) kan verdeeld worden in \(11\) kleinere, verschillende vierkanten met zijden \(99,78,21,57,77,43,16,41,34,9,25\)

(Rectangle/Squares Problem) (Presque carrés parfaits 176 x 177 - Ordre 11)

Een magisch vierkant van orde \(3\) met enkel priemgetallen ; de rij-en kolomsom is \(177\) (zie ook 111.6 ) :

\(177\) is de kleinst mogelijke magische sum voor een dergelijk vierkant met priemgetallen.

\(177^2\mathbf{\color{blue}{\;=\;}}295^2-236^2\mathbf{\color{blue}{\;=\;}}1745^2-1736^2\mathbf{\color{blue}{\;=\;}}5223^2-5220^2\)

\(177^3\mathbf{\color{blue}{\;=\;}}2537^2-944^2\mathbf{\color{blue}{\;=\;}}5487^2-4956^2\mathbf{\color{blue}{\;=\;}}\cdots\mathbf{\color{blue}{\;=\;}}\bbox[2px,border:1px brown dashed]{15753^2-15576^2}\)

De eerste keer dat er \(177\) opeenvolgende samengestelde getallen voorkomen gebeurt tussen de priemgetallen \(39389989\)
en \(39390167\) met aldus een priemkloof van \(178\,.~~\) (OEIS A000101.pdf)

Elke binnenhoek van een reguliere \(120\)-hoek bedraagt \(177\) graden. (Internet bron)

Voor \(n=177~~\) geldt \(~~{\large\sigma}(n)={\large\sigma}(n+26) ~~\to~~ {\large\sigma}(177)={\large\sigma}(203)=240~~~~({\large\sigma}\) of  'sigma' staat voor som der delers)

\(177\) is de derde oplossing uit de reeks \(99,150,177,220,429,539,623,702,1184,1338,\ldots\)

\(\begin{align}177\mathbf{\color{blue}{\;=\;}}\left({\frac{1587207867247}{468227201520}}\right)^3+\left({\frac{2419913540753}{468227201520}}\right)^3\end{align}\)

(Integral Sum of Two Rational Cubes) (OEIS A020898) (OEIS A228499)

\((x^3+y^3)/z^3=n~\to~\) [x waarde] (OEIS A190356)  [y waarde] (OEIS A190580)  [z waarde] (OEIS A190581)

Kleinste positieve oplossingen \(~\to~\) [x waarde] (OEIS A254326)  [y waarde] (OEIS A254324)