Allemaal Getallen Index 0049

$49 \mathbf{\color{blue}{\;=\;}}4+5+6+7+8+9+10\mathbf{\color{blue}{\;=\;}}24+25$ (som van opeenvolgende gehele getallen)

$49=1+3+5+7+9+11+13$ (som van opeenvolgende onpare getallen)

$49\mathbf{\color{blue}{\;=\;}}21+28\mathbf{\color{blue}{\;=\;}}D(6)+D(7)$ (som van opeenvolgende driehoeksgetallen)

$49=13+17+19$ ($49$ is ook het kleinste kwadraat dat de som is van opeenvolgende priemgetallen)

$49\mathbf{\color{blue}{\;=\;}}$op verschillende wijzen te schrijven als som van kwadraten. Vertrekkend van bvb.

$\qquad\;\,49=9*1^2+10*2^2~~$ kan men door samennemen het aantal termen verminderen. Enkele voorbeelden zijn :

$\qquad\;\,6*1^3+2*2^3+3^3\mathbf{\color{blue}{\;=\;}}9*1^3+5*2^3$

$49={\Large\frac{\,1^3+3^3+5^3+7^3+9^3}{1\,+\,3\,+\,5\,+\,7\,+\,9}}$ (OEIS A056220)

$49=3^2+5^2+3*5$

$49=((0;0;0;7)\,(0;2;3;6)\,(1;4;4;4)\,(2;2;4;5))\lower2pt{\Large{\color{teal}{➋}}}\to\{\#4\}$

$49=1^4+2^4+2^4+2^4$

$49=11*5-7+3-2$ (expressie met de vijf eerste priemgetallen)

$49\mathbf{\color{blue}{\;=\;}}1^3+2^3+2^3+2^3+2^3+2^3+2^3\mathbf{\color{blue}{\;=\;}}1^3+1^3+1^3+1^3+1^3+1^3+2^3+2^3+3^3\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,((0;0;1;2;2;2;2;2;2)\,(1;1;1;1;1;1;2;2;3))\lower2pt{\Large{\color{teal}{➌}}}\to\{\#2\}$

$49\mathbf{\color{blue}{\;=\;}}[3^4][9^2]-2^5\mathbf{\color{blue}{\;=\;}}\bbox[2px,border:1px brown dashed]{[5^4][25^2]-24^2}\mathbf{\color{blue}{\;=\;}}65^3-524^2$

49.1

$49\mathbf{\color{blue}{\;=\;}}$(som van drie derdemachten)

$\qquad\;\,$References Sum of Three Cubes

$\qquad\;\,$Getallen van de vorm $~9m+4~$ of $~9m+5~$ kunnen nooit als som van drie derdemachten geschreven worden.

$\qquad\;\,$In dit geval is $m=5~~(+4)$.

$49\mathbf{\color{blue}{\;=\;}}$(som van vier derdemachten)

$\qquad\;\,(z\gt1000)$

$\qquad\;\,\bbox[3px,border:1px solid]{1^3+(-2)^3+(-2)^3+4^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-5)^3+7^3+7^3+(-8)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-11)^3+13^3+16^3+(-17)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{10^3+10^3+25^3+(-26)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{1^3+(-23)^3+(-26)^3+31^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-2)^3+25^3+34^3+(-38)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-5)^3+31^3+34^3+(-41)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{4^3+(-23)^3+(-44)^3+46^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-32)^3+34^3+46^3+(-47)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{19^3+19^3+67^3+(-68)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{22^3+(-44)^3+(-68)^3+73^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-26)^3+52^3+73^3+(-80)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-44)^3+(-62)^3+(-71)^3+88^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-68)^3+70^3+97^3+(-98)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-26)^3+(-50)^3+(-95)^3+100^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{28^3+73^3+112^3+(-122)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{31^3+(-50)^3+(-125)^3+127^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{1^3+(-86)^3+(-116)^3+130^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-47)^3+(-68)^3+(-128)^3+136^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{37^3+85^3+124^3+(-137)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-86)^3+(-110)^3+(-119)^3+154^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-5)^3+(-71)^3+(-152)^3+157^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-2)^3+(-95)^3+(-185)^3+193^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-41)^3+61^3+229^3+(-230)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-59)^3+(-200)^3+(-227)^3+271^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-239)^3+244^3+268^3+(-272)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-191)^3+193^3+271^3+(-272)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-197)^3+(-230)^3+(-233)^3+319^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-122)^3+(-239)^3+(-275)^3+331^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{4^3+262^3+265^3+(-332)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{52^3+58^3+334^3+(-335)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{61^3+(-188)^3+(-317)^3+337^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-8)^3+(-167)^3+(-326)^3+340^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{169^3+232^3+286^3+(-344)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-5)^3+(-170)^3+(-335)^3+349^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-47)^3+(-260)^3+(-296)^3+352^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-62)^3+(-143)^3+(-359)^3+367^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{7^3+259^3+319^3+(-368)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-23)^3+(-251)^3+(-338)^3+379^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-146)^3+169^3+376^3+(-380)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-2)^3+76^3+382^3+(-383)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-95)^3+232^3+358^3+(-386)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{7^3+(-98)^3+(-395)^3+397^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-50)^3+292^3+337^3+(-398)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-80)^3+(-239)^3+(-368)^3+400^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-137)^3+292^3+379^3+(-425)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-71)^3+193^3+412^3+(-425)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-173)^3+355^3+388^3+(-461)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{193^3+355^3+373^3+(-470)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{1^3+(-110)^3+(-470)^3+472^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{157^3+(-299)^3+(-449)^3+484^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{7^3+(-116)^3+(-509)^3+511^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{103^3+241^3+505^3+(-524)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{370^3+(-410)^3+(-503)^3+526^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{190^3+(-278)^3+(-527)^3+544^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-71)^3+358^3+514^3+(-566)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-401)^3+403^3+568^3+(-569)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-2)^3+190^3+568^3+(-575)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-164)^3+(-359)^3+(-521)^3+577^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{61^3+(-173)^3+(-572)^3+577^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-44)^3+337^3+544^3+(-584)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{34^3+436^3+505^3+(-596)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{154^3+(-356)^3+(-560)^3+601^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{124^3+232^3+601^3+(-614)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-110)^3+(-290)^3+(-599)^3+622^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-71)^3+472^3+562^3+(-656)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-44)^3+445^3+583^3+(-659)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-11)^3+379^3+628^3+(-671)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-158)^3+280^3+673^3+(-686)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-239)^3+436^3+640^3+(-692)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-26)^3+520^3+580^3+(-695)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-122)^3+475^3+613^3+(-695)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-80)^3+(-428)^3+(-638)^3+697^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-83)^3+(-317)^3+(-674)^3+697^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{220^3+(-524)^3+(-590)^3+697^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{94^3+469^3+637^3+(-713)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{124^3+268^3+730^3+(-743)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{148^3+202^3+736^3+(-743)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-212)^3+(-362)^3+(-719)^3+754^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-332)^3+(-482)^3+(-674)^3+769^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-224)^3+307^3+763^3+(-773)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-197)^3+541^3+697^3+(-788)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-452)^3+(-488)^3+(-662)^3+793^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-197)^3+298^3+787^3+(-797)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{73^3+532^3+742^3+(-824)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-437)^3+(-479)^3+(-722)^3+829^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-2)^3+(-161)^3+(-833)^3+835^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-38)^3+556^3+778^3+(-863)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{202^3+241^3+856^3+(-866)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-266)^3+(-503)^3+(-812)^3+880^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-53)^3+430^3+865^3+(-899)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{10^3+289^3+892^3+(-902)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-95)^3+(-638)^3+(-782)^3+904^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{364^3+571^3+805^3+(-911)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-245)^3+460^3+883^3+(-917)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-443)^3+(-623)^3+(-782)^3+931^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{199^3+697^3+778^3+(-935)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-395)^3+(-461)^3+(-872)^3+937^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{766^3+(-860)^3+(-860)^3+937^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-398)^3+700^3+817^3+(-938)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-98)^3+538^3+889^3+(-950)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-71)^3+(-278)^3+(-950)^3+958^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{505^3+(-734)^3+(-872)^3+976^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{505^3+658^3+808^3+(-980)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-212)^3+(-431)^3+(-950)^3+982^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-200)^3+748^3+814^3+(-983)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-80)^3+622^3+892^3+(-983)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{79^3+271^3+982^3+(-989)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-2)^3+361^3+982^3+(-998)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{349^3+(-725)^3+(-887)^3+1012^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-419)^3+(-593)^3+(-947)^3+1042^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-443)^3+(-647)^3+(-941)^3+1060^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{46^3+(-599)^3+(-992)^3+1060^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{475^3+853^3+865^3+(-1112)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-410)^3+(-839)^3+(-986)^3+1174^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{157^3+919^3+949^3+(-1178)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{571^3+928^3+955^3+(-1229)^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,\bbox[3px,border:1px green solid]{(-815)^3+(-941)^3+(-998)^3+1333^3}\mathbf{\color{blue}{\;=\;}}$

$\qquad\;\,(z\gt1000)$

$49\mathbf{\color{blue}{\;=\;}}$(som van vijf vijfdemachten)

$\qquad\;\,$(fully searched up to $z=1000)$

$\qquad\;\,\bbox[lightyellow,3px,border:1px blue solid]{~oplossing~onbekend~}\mathbf{\color{blue}{\;=\;}}$

49.2

$49^2\mathbf{\color{blue}{\;=\;}}14^3-7^3\mathbf{\color{blue}{\;=\;}}76^2-15^3\mathbf{\color{blue}{\;=\;}}175^2-168^2\mathbf{\color{blue}{\;=\;}}735^2-14^5\mathbf{\color{blue}{\;=\;}}1201^2-1200^2$

$49^3\mathbf{\color{blue}{\;=\;}}35^4-1176^2\mathbf{\color{blue}{\;=\;}}98^3-7^7\mathbf{\color{blue}{\;=\;}}1029^2-98^3\mathbf{\color{blue}{\;=\;}}\bbox[2px,border:1px brown dashed]{1225^2-1176^2}\mathbf{\color{blue}{\;=\;}}8407^2-8400^2$

49.3

De breuk $49/98$ kan “vereenvoudigd” worden door in teller en noemer de $9$ te schrappen. Inderdaad,
$\require{cancel}{\Large{{\frac{\,4\!\cancel{\color{red}{9}}}{\!\cancel{\color{red}{9}}\!8}}}}=49/98=4/8\;(=1/2)$. Het is ten stelligste af te raden deze “techniek van vereenvoudiging” te veralgemenen !
Zie ook bij

49.4

De samenstellende cijfers van $49$ zijn kwadraten ($4=2^2$ en $9=3^2\,)$ en bovendien is $49$ ook een kwadraat en
het product van de cijfers : $4*9=36=6^2$. Zie ook en

49.5

De oneven machten van $49$ eindigen op $49$; de even machten eindigen op $01$.

49.6

$49=4*9+4+9$ (zie bij )

49.7

○–○–○

$\sqrt{49}=4+\sqrt9=-\sqrt{4}+9=7.~~~~$ Zie ook bij (RightClick + Esc)
$49^2=2401~~$ en $~~24*prime(0!)+1=49$
$49^3=117649~~$ en $~~1+1+7*6-4+9=49$
$49^4=5764801~~$ en $~~-5+7*6+4+8-0!+1=49$
$49^5=282475249~~$ en $~~2-8-2+47-5+2+4+9=49$
$49^6=13841287201~~$ en $~~1-3-8+41+2+8+7+2+0-1=49$
$49^7=678223072849~~$ en $~~6+7-8-2-2-3+0+72-8-4-9=49$
$49^8=33232930569601~~$ en $~~3+3+2+32+9+3+0+5+6-9-6+0+1=49$
$49^9=1628413597910449~~$ en $~~1+6+2-8-4+1+3+5+9+7+9+1+0+4+4+9=49$

49.8

$\underline{49}^3=1176\underline{49}$ en deze derdemacht kan opgesplitst worden in drie kwadraten : $[1][1764][9]$ (zijnde $[1^2][42^2][3^2]$)

49.9

Een uitdrukking als $2$$^{(3a+3)}$$-7*a-8$ is steeds deelbaar door $49$. Bvb. met $a=2$ komt er :
$2^9-7*2-8=512-14-8=490=49*10$

49.10

Er zijn twee rechthoekige driehoeken met gehele zijden en waarvan één zijde $49$ is :
$(49;168;175),(49;1200;1201)$

49.11

$1/49=0,\overline{020408163265306122448979591836734693877551}\;\overline{0204081632653061224489\ldots}$ (periode $42$).
Dit getal is opgebouwd uit opeenvolgende machten van $2$ in de decimalen :

\begin{align} &0,0\mathbf{2}\\ &0,000\mathbf{4}\\ &0,00000\mathbf{8}\\ &0,000000\mathbf{16}\\ &0,00000000\mathbf{32}\\ &0,0000000000\mathbf{64}\\ &0,00000000000\mathbf{128}\\ &0,0000000000000\mathbf{256}\\ &\cdots \end{align}

Opgeteld → $0,02040816326530\ldots=\Large{1\over49}$
Ook is $0,020408\ldots551*2=0,040816\ldots755102$ (cyclische permutatie); dit lukt met de $42$ positieve getallen
die $\lt49$ en copriem met $49$ zijn (copriem = geen gemeenschappelijke deler hebben, verschillend van $1$, m.a.w.
onderling ondeelbaar zijn)

49.12

\begin{align} 49&=7^2\\ 4489&=67^2\\ 444889&=667^2\\ 44448889&=6667^2\\ \cdots&=\cdots \end{align}

49.13

\begin{align} 49999999&=2+49999997~~&en\;omgekeerd&&~~99999994&=2*49999997\\ 4999999&=2+4999997~~&en\;omgekeerd&&~~9999994&=2*4999997\\ 499999&=2+499997~~&en\;omgekeerd&&~~999994&=2*499997\\ 49999&=2+49997~~&en\;omgekeerd&&~~99994&=2*49997\\ 4999&=2+4997~~&en\;omgekeerd&&~~9994&=2*4997\\ 499&=2+497~~&en\;omgekeerd&&~~994&=2*497\\ 49&=2+47~~&en\;omgekeerd&&~~94&=2*47 \end{align}

49.14

EEN SPELLETJE

Gooi twee dobbelstenen en noteer het aantal ogen van elk; maak het produkt van beide aantallen. Noteer het aantal
ogen aan de onderkant van beide stenen en maak hier ook het produkt van. Bereken het produkt van de ogen van de
ene dobbelsteen met de ogen aan de onderkant van de tweede dobbelsteen. Doe hetzelfde met de ogen van de andere
dobbelsteen met de ogen van de eerste dobbelsteen. Maak de som van de vier producten. Die som is steeds $49$.

Een voorbeeld :
We gooien :$\;\!\qquad3$ en $5\to3*5={\color{blue}{15}}$
Ogen onderaan : $4$ en $2\to4*2={\color{blue}{8}}$
Kruiselings vermenigvuldigen : $3*2={\color{blue}{6}}$ en $5*4={\color{blue}{20}}$
We hebben $15+8+6+20=49$

Dit spelletje is gebaseerd op het feit dat de som van de ogen van twee overstaande zijden van een dobbelsteen steeds $7$ is.
Noem $A$ en $B$ de gegooide ogen. Dan zijn $7-A$ en $7-B$ de ogen aan de overstaande zijden.
We berekenen dan : $AB+(7-A)(7-B)+A(7-B)+B(7-A)$ en dit is na uitwerking steeds $49$.

49.15

$49$ als resultaat met breuken waarin de cijfers van $1$ tot $9$ exact één keer voorkomen : ($geen$ oplossingen) :

$49$ als resultaat met breuken waarin de cijfers van $0$ tot $9$ exact één keer voorkomen : ($1$ oplossing) :
$197568/4032=49$

49.16

Men moet $49$ tot minimaal de $2392$ste macht verheffen opdat in de decimale expansie exact $49$ $49$'s verschijnen.
Terloops : $49$$^{2392}$ is $4043$ cijfers lang. Noteer dat $2392$ als $4043$ exact één keer voorkomen in de decimale expansie.

49.17

$49$ als som van twee priemgetallen kan enkel als volgt :

$$ 2~primes\\ \left[ \begin{matrix} \\ &2&+&47\\ \\ \end{matrix} \right. $$

$49$ als som van drie oneven priemgetallen.
In vet staan de acht sommen aangegeven met verschillende priemgetallen :

$$ 3~odd~primes \left[ \begin{matrix} &3&+&3&+&43\\ &&\mathbf{3}&+&\mathbf{5}&+&\mathbf{41}\\ &&\mathbf{3}&+&\mathbf{17}&+&\mathbf{29}\\ &3&+&23&+&23\\ &&\mathbf{5}&+&\mathbf{7}&+&\mathbf{37}\\ &&\mathbf{5}&+&\mathbf{13}&+&\mathbf{31}\\ &&\mathbf{7}&+&\mathbf{11}&+&\mathbf{31}\\ &&\mathbf{7}&+&\mathbf{13}&+&\mathbf{29}\\ &&\mathbf{7}&+&\mathbf{19}&+&\mathbf{23}\\ &11&+&19&+&19\\ &13&+&13&+&23\\ &&\mathbf{13}&+&\mathbf{17}&+&\mathbf{19} \end{matrix} \right. $$

49.18

Multigrades :

$$ 49 = \left| \begin{matrix} &9+40~~&&en&&~~9^2+40^2=1681=41^2\\ &&&maar~ook\\ &21+28~~&&en&&~~21^2+28^2=1225=35^2 \end{matrix} \right. $$

$$ 49 = \left| \begin{matrix} &7^1+18^1+24^1&=&8^1+14^1+27^1&=&9^1+12^1+28^1\\ &&&en\\ &7^2+18^2+24^2&=&8^2+14^2+27^2&=&9^2+12^2+28^2 \end{matrix} \right. $$

49.19

Als som met de vier operatoren $+-*\;/$
$49=(6+6)+(6-6)+(6*6)+(6/6)$

49.20

De eerste keer dat er $49$ opeenvolgende samengestelde getallen voorkomen gebeurt tussen de priemgetallen $31907$
en $31957$ met aldus een priemkloof van $50\,.~~$ (OEIS A000101.pdf)

49.21

$49$ is het kleinste getal met de eigenschap waarbij hijzelf en zijn directe buren kwadratisch zijn. In andere woorden,

elk van deze getallen bevat minstens één kwadraat in zijn factorisatie.

$48=2^2*2^2*3$

$49=7^2$

$50=2*5^2$

49.22

$49=7^2={\Large\frac{8!\,-\,7!}{6!}}$

49.23

$100$$^{49}$$\,+\,49$ is een priemgetal, de vierde in zijn soort ($100^k+k$).

De reeks gaat als volgt $k=1,3,9,49,\ldots$

49.24

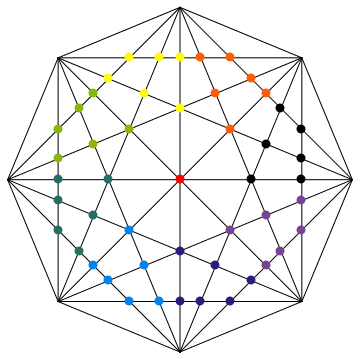
$49$ is het aantal snijpunten gemaakt door de diagonalen binnen in een reguliere achthoek.

(OEIS A006561)

49.25

$49$$^{49}$$-2$ is een priemgetal, de zesde in zijn soort ($k^k-2$). (OEIS A100408)

49.26

Som der reciproken van partitiegetallen van $49$ is $1$ op zeven wijzen

Er zijn geen partities met unieke termen.

$(1)~~49=3+4+6+12+12+12~~$ en $~~1={\Large\frac{1}{3}}+{\Large\frac{1}{4}}+{\Large\frac{1}{6}}+{\Large\frac{1}{12}}+{\Large\frac{1}{12}}+{\Large\frac{1}{12}}$

$(2)~~49=4+4+4+10+12+15~~$ en $~~1={\Large\frac{1}{4}}+{\Large\frac{1}{4}}+{\Large\frac{1}{4}}+{\Large\frac{1}{10}}+{\Large\frac{1}{12}}+{\Large\frac{1}{15}}$

$(3)~~49=4+4+5+6+15+15~~$ en $~~1={\Large\frac{1}{4}}+{\Large\frac{1}{4}}+{\Large\frac{1}{5}}+{\Large\frac{1}{6}}+{\Large\frac{1}{15}}+{\Large\frac{1}{15}}$

$(4)~~49=4+4+5+8+8+20~~$ en $~~1={\Large\frac{1}{4}}+{\Large\frac{1}{4}}+{\Large\frac{1}{5}}+{\Large\frac{1}{8}}+{\Large\frac{1}{8}}+{\Large\frac{1}{20}}$

$(5)~~49=4+4+6+7+7+21~~$ en $~~1={\Large\frac{1}{4}}+{\Large\frac{1}{4}}+{\Large\frac{1}{6}}+{\Large\frac{1}{7}}+{\Large\frac{1}{7}}+{\Large\frac{1}{21}}$

$(6)~~49=4+5+5+5+10+20~~$ en $~~1={\Large\frac{1}{4}}+{\Large\frac{1}{5}}+{\Large\frac{1}{5}}+{\Large\frac{1}{5}}+{\Large\frac{1}{10}}+{\Large\frac{1}{20}}$

$(7)~~49=7+7+7+7+7+7+7~~$ en $~~1={\Large\frac{1}{7}}+{\Large\frac{1}{7}}+{\Large\frac{1}{7}}+{\Large\frac{1}{7}}+{\Large\frac{1}{7}}+{\Large\frac{1}{7}}+{\Large\frac{1}{7}}$

(OEIS A125726)

49.27

${\color{blue}{49}}+50+51+52+53+54+55+56=57+58+59+60+61+62+63={\color{tomato}{420}}$

Gelijkheid van twee sommen met doorlopend opeenvolgende gehele getallen.

Dit is een eigenschap van de kwadraten zoals $k=49=7^2$. De linkersom heeft $\sqrt{k}+1$ termen en de rechtersom $\sqrt{k}$.

(OEIS A059270)

49.28

$\begin{align}49\mathbf{\color{blue}{\;=\;}}\left({\frac{11}{3}}\right)^3-\left({\frac{2}{3}}\right)^3\mathbf{\color{blue}{\;=\;}}\left({\frac{5308}{4017}}\right)^3+\left({\frac{14465}{4017}}\right)^3\end{align}$

(Integral Sum of Two Rational Cubes) (OEIS A020898) (OEIS A228499) (Links uit OEIS A060838)

$(x^3+y^3)/z^3=n~\to~$ [x waarde] (OEIS A190356) [y waarde] (OEIS A190580) [z waarde] (OEIS A190581)

Kleinste positieve oplossingen $~\to~$ [x waarde] (OEIS A254326) [y waarde] (OEIS A254324)

49.29

De expressie $~~2$$^{3*n+3}$$\,-\,7*n-8~~$ is steeds deelbaar door $49$.

49.30

$49$$^{6}$$+49$$^{7}$$+49$$^{8}$$+49$$^{5}$$+49$$^{0}$$+49$$^{2}$$+49$$^{7}$$+49$$^{8}$$+49$$^{1}$$+49$$^{0}$$+49$$^{4}$$+49$$^{2}$$+49$$^{0}$$+49$$^{6}$$\mathbf{\color{blue}{\;=\;}}67850278104206~~$(OEIS A236067)

49.31

Som Der Cijfers ($sdc$) van $k^{\large{49}}$ is gelijk aan het grondtal $k$. De triviale oplossingen $0$ en $1$ negerend vinden we :

$\qquad\qquad~sdc\left(270^{\large{49}}\right)=270\qquad\qquad~sdc\left(290^{\large{49}}\right)=290\qquad\qquad~sdc\left(340^{\large{49}}\right)=340$

$\qquad\qquad~sdc\left(350^{\large{49}}\right)=350\qquad\qquad~sdc\left(360^{\large{49}}\right)=360\qquad\qquad~sdc\left(533^{\large{49}}\right)=533$

$\qquad\qquad~sdc\left(589^{\large{49}}\right)=589\qquad\qquad~sdc\left(637^{\large{49}}\right)=637\qquad\qquad~sdc\left(648^{\large{49}}\right)=648$

$\qquad\qquad~sdc\left(661^{\large{49}}\right)=661\qquad\qquad~sdc\left(695^{\large{49}}\right)=695$

49.32

Expressie met tweemaal de cijfers uit het getal $49$ enkel met operatoren $+,-,*,/,()$
$49=4*9+4+9$

49.33

Elk natuurlijk getal is de som van $49$ palindromen (0 incl.)
(Web-bron)

49.34

Als expressie met enkelcijferige toepassing, resp. van $1$ tot $9~~$ (met dank aan Inder. J. Taneja).
$\qquad\qquad49=(11-1)^{(1+1)}/(1+1)-1$
$\qquad\qquad49=2*(22+2)+2/2$
$\qquad\qquad49=3^3+33-33/3$
$\qquad\qquad49=4+44+4/4$
$\qquad\qquad49=55-5-5/5$
$\qquad\qquad49=6*6+6+6+6/6$
$\qquad\qquad49=7*7$
$\qquad\qquad49=8*8-8-8+8/8$
$\qquad\qquad49=(9*99-9)/(9+9)$

49.35

Met de cijfers van $1$ tot $9$ in stijgende en dalende volgorde (met dank aan Inder. J. Taneja) :
$\qquad\qquad49=1*2+3*4+5+6+7+8+9$
$\qquad\qquad49=9+8+7+6+5+4*3+2*1$

49.36

Het kleinste getal dat exact $49$ delers heeft is $46656=2^6*3^6$. (OEIS A005179)

49.37

$49$ is het product van $28$ ( driehoeksgetal van rang $7~$) met de som van de reciproken van de $7$ kleinste
driehoeksgetallen: $28*({\Large\frac{1}{1}+\frac{1}{3}+\frac{1}{6}+\frac{1}{10}+\frac{1}{15}+\frac{1}{21}+\frac{1}{28}})=49$

49.38

(drie multigrades) $49\to49^5\to$

\begin{aligned} 49^1&=39^1-75^1+92^1+100^1-107^1\\ 49^5&=39^5-75^5+92^5+100^5-107^5\\ \\ 49^1&=-143^1-342^1+562^1+764^1-792^1\\ 49^5&=-143^5-342^5+562^5+764^5-792^5\\ \\ 49^1&=33^1-595^1+619^1+795^1-803^1\\ 49^5&=33^5-595^5+619^5+795^5-803^5\\ \end{aligned}

49.39

$49$ is het aantal oplichtende of fluorescerende LED segmentjes in onderstaande display van de cijfers van $0$ tot $9$.

Cijfer $7$ wordt op twee manieren weergegeven, één met $3$ segmentjes zoals hierboven en één met $4$ zoals bij
Wikipedia - Zevensegmentendisplay

49.40

\(49\)	\(7^2\)	\(3\)	\(57\)
	\(1,7,49\)
	\(110001_2\)	\(61_8\)	\(31_{16}\)
			\(49=7^2\)

radix	omzetting	radix	omzetting
2		20
3		21
4		22
5		23
6		24
7		25
8		26
9		27
10		28
11		29
12		30
13		31
14		32
15		33
16		34
17		35
18		36
19		F5 = CLEAR