\(12=3+4+5\) (som van opeenvolgende gehele getallen). Opmerkelijk is dat het omgekeerde getal \(21=6+7+8\) \(\qquad\;\,\)ook een som van opeenvolgende gehele getallen is. \(12=2+4+6\) (som van opeenvolgende pare getallen) \(12=5+7\) (som van opeenvolgende onpare getallen) (som van opeenvolgende priemgetallen) \(12=1+1+2+3+5\) (som van opeenvolgende Fibonaccigetallen) \(12\mathbf{\color{blue}{\;=\;}}2^2+2^2+2^2\mathbf{\color{blue}{\;=\;}}1^2+1^2+1^2+3^2\mathbf{\color{blue}{\;=\;}}((0;2;2;2)\,(1;1;1;3))\lower2pt{\Large{\color{teal}{➋}}}\to\{\#2\}\) \(12=1!*2!*3!\) \(12=1^0+2^1+3^2\) \(12\mathbf{\color{blue}{\;=\;}}1^3+1^3+1^3+1^3+2^3\mathbf{\color{blue}{\;=\;}}(0;0;0;0;1;1;1;1;2)\lower2pt{\Large{\color{teal}{➌}}}\to\{\#1\}\) \(12=1^3*2^2*3^1\) (symmetrische uitdrukking : grondtal opgaand; exponent dalend) \(12\mathbf{\color{blue}{\;=\;}}3+3^2\mathbf{\color{blue}{\;=\;}}4^2-4\) \(12\mathbf{\color{blue}{\;=\;}}2^2+2^3\mathbf{\color{blue}{\;=\;}}[2^4][4^2]-2^2\mathbf{\color{blue}{\;=\;}}47^2-13^3\) | 12.1 |
\(12\mathbf{\color{blue}{\;=\;}}\)(som van drie derdemachten) \(\qquad\;\,2\) oplossingen bekend \(\qquad\;\,\)References Sum of Three Cubes \(\qquad\;\,\bbox[3px,border:1px solid]{7^3+10^3+(-11)^3}\mathbf{\color{blue}{\;=\;}}\) \(\qquad\;\,\bbox[3px,border:1px solid]{(-5725013)^3+(-9019406)^3+9730705^3}\mathbf{\color{blue}{\;=\;}}\) \(12\mathbf{\color{blue}{\;=\;}}\)(som van vijf vijfdemachten) \(\qquad\;\,\bbox[3px,border:1px blue solid]{13^5+16^5+(-17)^5+k^5+(-k)^5}\mathbf{\color{blue}{\;=\;}}\to~~\)Noteer dat\(~~13+16-17+k-k\mathbf{\color{blue}{\;=\;}}12\) \(\qquad\;\,\bbox[3px,border:1px blue solid]{3^5+4^5+6^5+6^5+(-7)^5}\mathbf{\color{blue}{\;=\;}}\to~~\)Noteer dat\(~~3+4+6+6-7\mathbf{\color{blue}{\;=\;}}12\) \(\qquad\;\,\bbox[3px,border:1px blue solid]{16^5+(-35)^5+95^5+138^5+(-142)^5}\mathbf{\color{blue}{\;=\;}}(z\gt200)\) | 12.2 |
\(12=(1+2)+(1^3+2^3)\) ( Er zijn \(6\) getallen met deze eigenschap : getal = som van de cijfers plus som van \(\qquad\,\) de derdemachten van de cijfers; die getallen zijn : \(12,30,666,870,960\) en \(1998\) ) (OEIS A065138) | 12.3 |
| Sporen van het twaalftallig rekenstelsel zijn nog te vinden in de dag- en nachtindeling in telkens \(12\) uren. Ook in de maten en gewichten komen er nog verwijzingen naar \(12\) voor : een dozijn, een gros \((144=12^2\,)\) | 12.4 |
| \(12\) is het kleinste getal met exact \(6\) delers. (OEIS A005179) Het product van de echte delers van \(12\) is zijn kwadraat \(~1*2*3*4*6=144=12^2\) De som van de echte delers van \(12\) is een kwadraat \(~1+2+3+4+6=16=4^2\) \(12\) is het kleinste getal dat gelijk is aan de som van een aantal van zijn niet-triviale delers : \(2+4+6=12\) \(12\) is gelijk aan de som van \(3\) Fibonaccigetallen : \(12=1+3+8\) | 12.5 |
| \(12\) als som van twee priemgetallen (bovendien zijn beide getallen oneven) :
$$ 2~odd~primes \left[ \begin{matrix} \\ &5&+&7\\ \\ \end{matrix} \right. $$ \(12\) als som van drie priemgetallen (die bij de bovenste som bovendien verschillend zijn) :$$ 3~primes \left[ \begin{matrix} &&\mathbf{2}&+&\mathbf{3}&+&\mathbf{7}\\ \\ &2&+&5&+&5 \end{matrix} \right. $$ | 12.6 |
\(12\) is gelijk aan \(4\) maal de som van zijn cijfers : \(12=4*(1+2)\). Andere getallen met deze eigenschap zijn veelvouden van \(12\), namelijk \(24, 36\) en \(48~~\) ( ) Zie ook bij | 12.7 |
\(12=(5-1)*(5-2)\) | |
\(12=(1+2+3)*2\) \(12=3*4\) (dus een pronic getal) (vier opeenvolgende cijfers) (Fun With Num3ers) \(\qquad\;\,\)Dit patroon doet zich enkel nog voor bij \(12=(6*6*6)/(6+6+6)\) \(12!+34567\) is een priemgetal (\(479036167\)) \(12\mathbf{\color{blue}{\;=\;}}1+1+1+1+2+6\mathbf{\color{blue}{\;=\;}}1*1*1*1*2*6\) \(12\mathbf{\color{blue}{\;=\;}}1+1+1+1+1+3+4\mathbf{\color{blue}{\;=\;}}1*1*1*1*1*3*4\) | 12.8 |
| De som van twee priemtweelingen (groter dan \(3\)) is deelbaar door \(12\). Bvb. de priemtweelingen \(5867\) en \(5869\) : \(5867+5869=11736=12*978\) | 12.9 |
| \(12\) is ook een deler van het product van drie opeenvolgende getallen \((A-1)*A*(A+1)\) op voorwaarde dat \(A\) (= het middelste getal van de drie) oneven is (men heeft dan het product van een even, een oneven en nog een even getal). Bvb. met \(A=29\) komt er : \(28*29*30=24360=12*2030\) | 12.10 |
| In de bewerking \(12=3*4\) staan vier opeenvolgende getallen. Dit feit doet zich enkel nog voor met \(56=7*8\) | 12.11 |
\(12\) is één van de \(8\) getallen van \(2\) verschillende cijfers dat gelijk is aan een ééncijferig veelvoud van het cijfer van de eenheden : \(12=6*2\). De andere getallen zie bij | 12.12 |
| \(12\) kan niet geschreven worden als som van verschillende driehoeksgetallen. Zie voor meer toelichting bij | 12.13 |
| Als men van \(12\) het product maakt van al zijn delers dan krijgt men een macht van \(12\) : \(1*2*3*4*6*12=\) \(1728=12^3\). Soortgelijk patroon vindt men bij andere veelvouden van \(12\) die geen kwadraat zijn (uiteraard zal de exponent hoger zijn dan \(3\); de exponent is immers gelijk aan de helft van het aantal delers). Zie ook bij | 12.14 |
| Alle pare machten van \(12\), verminderd met \(1\), zijn deelbaar door \(143\) : bvb. \(12^4=20736\) en \(20735=143*145\) Alle onpare machten van \(12\), verminderd met \(1\) , zijn deelbaar door \(11\) : bvb. \(12^3=1728\) en \(1727=11*157\) De som van de cijfers van een willekeurige macht van \(12\) (met uitzondering van \(12^1\)) is een veelvoud van \(9\), bvb. \(12^5=248832~~\) en \(~~2+4+8+8+3+2=27=9*3\) | 12.15 |
\(12^2\mathbf{\color{blue}{\;=\;}}10^3-8^3-7^3-1^3\mathbf{\color{blue}{\;=\;}}10^3-9^3-7^3+6^3\). \(12^2=1*2*3*4*6\) (de \(5\) ontbreekt) = \(6!/5\) \(12^2=144\) en het omgekeerde is ook waar : \(21^2=441\) \(12^2+33^2=1233\). Zie ook bij \(12^3=9^3+10^3-1^3\) \(12^3=6^3+8^3+10^3\) (derdemachten van opeenvolgende pare getallen) | 12.16 |
\(12^2\mathbf{\color{blue}{\;=\;}}\to\) als som of verschil van twee machten zie bij paginagetal \(144\) \(12^3\mathbf{\color{blue}{\;=\;}}2^7+40^2\mathbf{\color{blue}{\;=\;}}42^2-6^2\mathbf{\color{blue}{\;=\;}}43^2-11^2\mathbf{\color{blue}{\;=\;}}48^2-24^2\mathbf{\color{blue}{\;=\;}}57^2-39^2\mathbf{\color{blue}{\;=\;}}62^2-46^2\mathbf{\color{blue}{\;=\;}}\bbox[2px,border:1px brown dashed]{78^2-66^2}\mathbf{\color{blue}{\;=\;}}112^2-104^2\mathbf{\color{blue}{\;=\;}}\) \(\qquad~~~147^2-141^2\mathbf{\color{blue}{\;=\;}}218^2-214^2\mathbf{\color{blue}{\;=\;}}\bbox[2px,border:1px brown dashed]{433^2-431^2}\) | 12.17 |
| \(12^5\mathbf{\color{blue}{\;=\;}}4^5+5^5+6^5+7^5+9^5+11^5\mathbf{\color{blue}{\;=\;}}248832\) is de kleinste vijfdemacht die de som van zes positieve vijfdemachten is. | 12.18 |
De volgende producten zijn symmetrisch ten opzichte van het gelijkheidsteken : \begin{align} 12*42&=24*21\to504\\ 12*63&=36*21\to736\\ 12*84&=48*21\to1008 \end{align} | 12.19 |
| \(12*23=276\gets\) leest van rechts naar links \(\to672=32*21\) | 12.20 |
| Palindromische vormen (met leidende nul) : \(12*\underline{0495=5940}\quad\) en \(\quad\underline{012*210}=\underline{120*021}\to2520\) | 12.21 |
| Het omgekeerde van \(12\) is \(21\); het omgekeerde van \(24\,(=2*12)\) is \(42\,(=2*21)\). Hetzelfde patroon heeft men met \(36\;(63)\) en \(48\;(84)\). | 12.22 |
| Alle cijfers van \(1\) tot \(9\) komen voor in \(12*483=5796\quad\) (Trouwens men heeft ook \(5796=42*183\)) | 12.23 |
\(12\to62\to\) \begin{align} 1^1+5^1+6^1&=2^1+3^1+7^1\\ en\;&ook\;is\\ 1^2+5^2+6^2&=2^2+3^2+7^2 \end{align} | 12.24 |
| \(12\) schrijven met behulp van de cijfers \(1,2,3\) en \(4\) : \(\quad(4-3)*12~~=~~1*2*3*\sqrt4~~=~~4^2-3-1~~=~~3^2+1+4-2~~=~~(2-1)*3*4~~=~~\) \(\quad2*(4+3-1)~~=~~2^4-1-3~~=~~(3*4)/(2-1)~~=~~4!/(3-2+1)\) Zie ook bij | 12.25 |
| \(12\) is het kleinste overvloedige getal (Eng: Abundant number) d.w.z. een getal dat kleiner is dan de som van zijn delers inclusief \(1\) en exclusief zichzelf. Zie ook bij (OEIS A005101) Kortom \(12 \to1+2+3+4+6=16\) en \(12\lt16\). | 12.26 |
| Er zijn \(12\) pentomino's (figuren bestaande uit vijf vierkanten die aan één of meer zijden samengevoegd zijn). Deze kunnen een totaal oppervlak van \(12*5=60\) eenheden bedekken, bvb. een rechthoek van \(3*20;4*15;5*12\) of \(6*10\). Tal van andere mogelijkheden bestaan. Zie illustratie bij en ook | 12.27 |
Twee driehoeken met zijden \((5;5;6)\) en \((5;5;8)\) hebben beide als oppervlakte een waarde van \(12\). Driehoeken met gehele zijden en waarvan de oppervlakte een geheel getal is, heten driehoeken van HERON (of HERO). | 12.28 |
| Er zijn vier rechthoekige driehoeken met gehele zijden en \(12\) als één van de zijden : \((5;12;13),(9;12;15),(12;16;20),(12;35;37)\) | 12.29 |
| Enkele getalpiramides \begin{align} 3*4&=12\\ 33*34&=1122\\ 333*334&=111222\\ 3333*3334&=11112222\\ \cdots&=\cdots \end{align} \begin{align} 1*9+2&=11\\ 12*9+3&=111\\ 123*9+4&=1111\\ 1234*9+5&=11111\\ 12345*9+6&=111111\\ 123456*9+7&=1111111\\ 1234567*9+8&=11111111\\ \cdots&=\cdots \end{align} \begin{align} 35^2&=1225\\ 335^2&=112225\\ 3335^2&=11122225\\ 33335^2&=1111222225\\ 333335^2&=111112222225\\ 3333335^2&=11111122222225\\ \cdots&=\cdots \end{align} | 12.30 |
| De som van de kwadraten van drie opeenvolgende oneven getallen, plus \(1\), is een veelvoud van \(12\). Men heeft in formulevorm : \((2n-1)^2+(2n+1)^2+(2n+3)^2=12n^2+12n+12=12*(n^2+n+1)\) | 12.31 |
| IETS SPECIAALS
Het getal \(12\) heeft \(6\) delers : \(1;2;3;4;6;12\). Het getal \(6\) is een perfect getal. De som Dit reuzengetal bestaat in feite uit een macht van \(2\), vermenigvuldigd met een aantal MERSENNE-priemgetallen. | 12.32 |
| MERKWAARDIG
Met de cijfers \(0,1\) en \(2\) voor de grondtallen en de cijfers \(0,1\) en \(4\) voor de kwadraten | 12.33 |
| Men moet \(12\) tot minimaal de \(588\)ste macht verheffen opdat in de decimale expansie exact \(12\) \(12\)'s verschijnen. Noteer, voor wat het waard is, dat \(588\) deelbaar is door \(12\to588/12=49\). Terloops : \(12\)\(^{588}\) is \(635\) cijfers lang. Getallen \(n\) waarbij het cijfer \(1\) niet voorkomt in de decimale expansie van \(n,n^2\) als \(n^3\) : \(588\to345744\to203297472~~\) en \(~~635\to403225\to256047875~~~~\) (OEIS A255357) | 12.34 |
Als som met de vier operatoren \(+-*\;/\) | 12.35 |
| \(12\) als resultaat met breuken waarin de cijfers van \(1\) tot \(9\) exact één keer voorkomen : (\(4\) oplossingen) \(45792/3816=73548/6129=89532/7461=91584/7632=12\) \(12\) als resultaat met breuken waarin de cijfers van \(0\) tot \(9\) exact één keer voorkomen : (\(1\) oplossing) \(107352/8946=12\) | 12.36 |
| Een hexaëder (kubus) heeft \(12\) ribben. Een icosaëder (twintigvlak) heeft \(12\) hoekpunten. \(12\) pentagons (vijfhoeken) zijn er nodig om een regelmatige dodecaëder (twaalfvlak) te vormen. 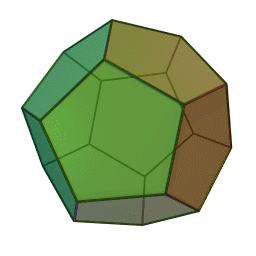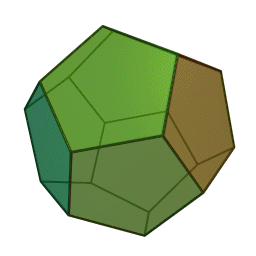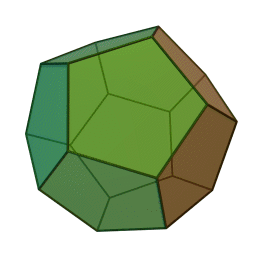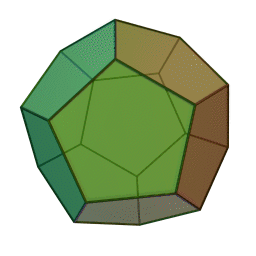 | 12.37 |
\(12!-1\) is een priemgetal \((=479001599)\), de vijfde in zijn soort \((k!-1)~~\) (OEIS A002982) | 12.38 |
Alle getallen van \(1\) tot \(12\) worden gebruikt, hetzij als grondtal hetzij als exponent, in deze gelijkheden van producten van machten. Vele andere combinaties zijn mogelijk. Verdeelsleutel \([1-5]\) levert geen oplossingen. Verdeelsleutel \([2-4]\) levert \(61\) zuivere oplossingen. Verdeelsleutel \([3-3]\) heeft er netto \(114\). \begin{align} 2^{10}*12^{11}&\mathbf{\color{blue}{\;=\;}}3^1*4^7*8^6*9^5\\ 2^{11}*3^7*4^{12}&\mathbf{\color{blue}{\;=\;}}6^5*8^{10}*9^1 \end{align} | 12.39 |
\(12\) als som van zes getallen (op een cirkel geplaatst) die één voor één het product zijn van hun buurgetallen \(12=6+2+{\Large\frac{1}{3}}+{\Large\frac{1}{6}}+{\Large\frac{1}{2}}+3\) | 12.40 |
\(10^2+11^2+{\color{blue}{12^2}}=13^2+14^2=\) | 12.41 |
\(\begin{align}12\mathbf{\color{blue}{\;=\;}}\left({\frac{19}{39}}\right)^3+\left({\frac{89}{39}}\right)^3\end{align}\) (Integral Sum of Two Rational Cubes) (OEIS A020898) (OEIS A228499) \((x^3+y^3)/z^3=n~\to~\) [x waarde] (OEIS A190356) [y waarde] (OEIS A190580) [z waarde] (OEIS A190581) Kleinste positieve oplossingen \(~\to~\) [x waarde] (OEIS A254326) [y waarde] (OEIS A254324) | 12.42 |
\(2\)\(^{12}\)\(\,+\,3\) is een priemgetal \((=4099)\), de zevende in zijn soort \((2^k+3)~~\) (OEIS A057732) \(2\)\(^{12}\)\(\,-\,3\) is een priemgetal \((=4093)\), de zevende in zijn soort \((2^k-3)~~\) (OEIS A050414) | 12.43 |
Som der reciproken van partitiegetallen van \(12\) levert nooit \(1\) op. Bijgevolg ook geen partities met unieke termen. | 12.44 |
○–○–○ \(12^2=144~~\) en \(~~(-1+4)*4=12\)\(12^3=1728~~\) en \(~~-1+7-2+8=12\) \(12^4=20736~~\) en \(~~2+0+7-3+6=12\) \(12^5=248832~~\) en \(~~2+4+8/8+3+2=12\) \(12^6=2985984~~\) en \(~~2*9-8+5+9-8-4=12\) \(12^7=35831808~~\) en \(~~3+5-8-3-1+8+0+8=12\) \(12^8=429981696~~\) en \(~~4+2+9-9+8+1-6+9-6=12\) \(12^9=5159780352~~\) en \(~~-5+15-9-7+8+0+3+5+2=12\) \(12^{10}=61917364224~~\) en \(~~619+1+7+3-642+24=12\) \(12^{11}=743008370688~~\) en \(~~74+30+0-8+3+7+0-6-88=12\) \(12^{12}=8916100448256~~\) en \(~~891+6-10+0-44-825-6=12\) \(12^{13}=106993205379072~~\) en \(~~10+6-9-9-3+2+0+5+3+7-9+0+7+2=12\) \(12^{14}=1283918464548864~~\) en \(~~12-8-3+9+1+8-46+4+5+4+8+8+6+4=12\) \(12^{15}=15407021574586368~~\) en \(~~15+4+0-7+0-2+1-5+74+5-8+6-3-68=12\) \(12^{16}=184884258895036416~~\) en \(~~18+48-8+4+2-58+89-50-36-4+1+6=12\) \(12^{17}=2218611106740436992~~\) en \(~~22+1+86+1-110+6+7+4+0-4+3-6+9-9+2=12\) \(12^{18}=26623333280885243904~~\) en \(~~266-233-33-2+8+0+88+5-2+4-3-90+4=12\) \(12^{19}=319479999370622926848~~\) en \(~~31+9-4+7+99-99-37+0+62+2-92-6-8+48=12\) \(12^{20}=3833759992447475122176~~\) en \(~~38+3-37+5+9-9-9+2+4+47+4+75-122+1+7-6=12\) | 12.45 |
Expressie met tweemaal de cijfers uit het getal \(12\) enkel met operatoren \(+,-,*,/,(),\)^^\(\) | 12.46 |
| \(12\) is de som van de termen van een priemtweelingenpaar \(5+7\) en \(12^2=144\) idem dito namelijk \(71+73~~\) (OEIS A213784) | 12.47 |
Som Der Cijfers (\(sdc\)) van \(k^{\large{12}}\) is gelijk aan het grondtal \(k\). De triviale oplossingen \(0\) en \(1\) negerend vinden we : \(\qquad\qquad~sdc\left(108^{\large{12}}\right)=108~~\to\) Unieke oplossing voor \(k\gt1\). Noteer dat \(108=12*(1+0+8)\) | 12.48 |
| Het kwadraat van \(12\) kan uitgedrukt worden als een som van verschillende faculteiten. \(12^2=144=4!+5!~~\) (OEIS A014597) In totaal zijn er maar \(15\) getallen van deze soort gekend. | 12.49 |
| Exponent \(12\) heeft geen groter grondtal dan \(4\) zodat de decimale expansie van deze macht geen cijfers bevat uit het grondtal\(~~~~\to~~~~4^{12}=16777216\) (OEIS A113951) | 12.50 |
\(12\) is een getal van de vorm \(2\)\(^k\)\(+k\)\(^3\), de derde in zijn soort. Reken uit met de waarde \(k=2~~\). (OEIS A097339) | 12.51 |
Als expressie met enkelcijferige toepassing, resp. van \(1\) tot \(9~~\) (met dank aan Inder. J. Taneja). | 12.52 |
Met de cijfers van \(1\) tot \(9\) in stijgende en dalende volgorde (met dank aan Inder. J. Taneja) : | 12.53 |
Expressie van \(n\) enkel gebruik makend van faculteiten, vierkantswortels en afrondingen. In Pari/GP code : \(12~=~\)floor(sqrt(sqrt(sqrt(12!)))) \(\qquad\qquad12={\huge\lfloor}\sqrt{\sqrt{\sqrt{12!}}}{\huge\rfloor}\) | 12.54 |
\({\Large\frac{400}{33}}=12,1212121212121212121212\ldots\) | 12.55 |
\({\Large\frac{1}{12^2}=\frac{1}{15^2}+\frac{1}{20^2}}~~~~\) (kleinste gehele getallen van de reciproke Pythagoras vergelijking) | 12.56 |
Het omgekeerde van \(4^{12}\) is een priemgetal \(\to{61277761}\) Pari/GP code : isprime(fromdigits(Vecrev(digits(4^12))))\(\to1=\) true | 12.57 |
Het omgekeerde van \(7^{12}\) is een priemgetal \(\to{10278214831}\) Pari/GP code : isprime(fromdigits(Vecrev(digits(7^12))))\(\to1=\) true | 12.58 |
| Het kleinste getal dat exact \(12\) delers heeft is \(60=2^2*3*5\). (OEIS A005179) | 12.59 |
| \(12\) is de omtrek van een rechthoekige driehoek met gehele zijden \((3;4;5)\). | 12.60 |