\(12\mathbf{\color{blue}{\;=\;}}3+4+5\) (som van opeenvolgende gehele getallen). Opmerkelijk is dat het omgekeerde getal \(21=6+7+8\) \(\qquad\;\,\)ook een som van opeenvolgende gehele getallen is. \(12\mathbf{\color{blue}{\;=\;}}2+4+6\) (som van opeenvolgende pare getallen) \(12\mathbf{\color{blue}{\;=\;}}5+7\) (som van opeenvolgende onpare getallen) (som van opeenvolgende priemgetallen) \(12\mathbf{\color{blue}{\;=\;}}1+1+2+3+5\) (som van opeenvolgende Fibonaccigetallen) \(12\mathbf{\color{blue}{\;=\;}}2^2+2^2+2^2\mathbf{\color{blue}{\;=\;}}1^2+1^2+1^2+3^2\mathbf{\color{blue}{\;=\;}}((0;2;2;2)\,(1;1;1;3))\lower2pt{\Large{\color{teal}{➋}}}\to\{\#2\}\) \(12\mathbf{\color{blue}{\;=\;}}1!*2!*3!\) \(12\mathbf{\color{blue}{\;=\;}}1^0+2^1+3^2\) \(12\mathbf{\color{blue}{\;=\;}}1^3+1^3+1^3+1^3+2^3\mathbf{\color{blue}{\;=\;}}(0;0;0;0;1;1;1;1;2)\lower2pt{\Large{\color{teal}{➌}}}\to\{\#1\}\) \(12\mathbf{\color{blue}{\;=\;}}1^3*2^2*3^1\) (symmetrische uitdrukking : grondtal opgaand; exponent dalend) \(12\mathbf{\color{blue}{\;=\;}}(6*6*6)/(6+6+6)\) \(12\mathbf{\color{blue}{\;=\;}}3+3^2\mathbf{\color{blue}{\;=\;}}4^2-4\) \(12\mathbf{\color{blue}{\;=\;}}(5-1)*(5-2)\) \(12\mathbf{\color{blue}{\;=\;}}(11+5)/2+7-3\) (expressie met de vijf eerste priemgetallen) \(12\mathbf{\color{blue}{\;=\;}}2*(1+2+3)\) \(12\mathbf{\color{blue}{\;=\;}}1+1+1+1+2+6\mathbf{\color{blue}{\;=\;}}1*1*1*1*2*6\) \(12\mathbf{\color{blue}{\;=\;}}1+1+1+1+1+3+4\mathbf{\color{blue}{\;=\;}}1*1*1*1*1*3*4\) \(12\mathbf{\color{blue}{\;=\;}}2^2+2^3\mathbf{\color{blue}{\;=\;}}[2^4][4^2]-2^2\mathbf{\color{blue}{\;=\;}}47^2-13^3\) | 12.1 |
\(12\mathbf{\color{blue}{\;=\;}}\)(som van drie derdemachten) \(\qquad\;\,2\) oplossingen bekend \(\qquad\;\,\)References Sum of Three Cubes \(\qquad\;\,\bbox[3px,border:1px solid]{7^3+10^3+(-11)^3}\mathbf{\color{blue}{\;=\;}}\) \(\qquad\;\,\bbox[3px,border:1px solid]{(-5725013)^3+(-9019406)^3+9730705^3}\mathbf{\color{blue}{\;=\;}}\) \(12\mathbf{\color{blue}{\;=\;}}\)(som van vijf vijfdemachten) \(\qquad\;\,\)(fully searched up to \(z=1000)\) \(\qquad\;\,\bbox[3px,border:1px blue solid]{13^5+16^5+(-17)^5+k^5+(-k)^5}\mathbf{\color{blue}{\;=\;}}\to~~\)Noteer dat\(~~13+16-17+k-k\mathbf{\color{blue}{\;=\;}}12\) \(\qquad\;\,\bbox[3px,border:1px blue solid]{3^5+4^5+6^5+6^5+(-7)^5}\mathbf{\color{blue}{\;=\;}}\to~~\)Noteer dat\(~~3+4+6+6-7\mathbf{\color{blue}{\;=\;}}12\) \(\qquad\;\,\bbox[3px,border:1px blue solid]{16^5+(-35)^5+95^5+138^5+(-142)^5}\mathbf{\color{blue}{\;=\;}}\) | 12.2 |
\(12^2\mathbf{\color{blue}{\;=\;}}\to\) als som of verschil van twee machten zie bij paginagetal \(144\) \(12^3\mathbf{\color{blue}{\;=\;}}2^7+40^2\mathbf{\color{blue}{\;=\;}}42^2-6^2\mathbf{\color{blue}{\;=\;}}43^2-11^2\mathbf{\color{blue}{\;=\;}}48^2-24^2\mathbf{\color{blue}{\;=\;}}57^2-39^2\mathbf{\color{blue}{\;=\;}}62^2-46^2\mathbf{\color{blue}{\;=\;}}\bbox[2px,border:1px brown dashed]{78^2-66^2}\mathbf{\color{blue}{\;=\;}}112^2-104^2\mathbf{\color{blue}{\;=\;}}\) \(\qquad~~~147^2-141^2\mathbf{\color{blue}{\;=\;}}218^2-214^2\mathbf{\color{blue}{\;=\;}}\bbox[2px,border:1px brown dashed]{433^2-431^2}\) | 12.3 |
| Sporen van het twaalftallig rekenstelsel zijn nog te vinden in de dag- en nachtindeling in telkens \(12\) uren. Ook in de maten en gewichten komen er nog verwijzingen naar \(12\) voor : een dozijn, een gros \((144=12^2\,)\) | 12.4 |
| \(12\) is het kleinste getal met exact \(6\) delers. (OEIS A005179) Het product van de echte delers van \(12\) is zijn kwadraat \(~1*2*3*4*6=144=12^2\) De som van de echte delers van \(12\) is een kwadraat \(~1+2+3+4+6=16=4^2\) \(12\) is het kleinste getal dat gelijk is aan de som van een aantal van zijn niet-triviale delers : \(2+4+6=12\) \(12\) is gelijk aan de som van \(3\) Fibonaccigetallen : \(12=1+3+8\) | 12.5 |
| \(12\) als som van twee priemgetallen (bovendien zijn beide getallen oneven) :
$$ 2~odd~primes \left[ \begin{matrix} \\ &5&+&7\\ \\ \end{matrix} \right. $$ \(12\) als som van drie priemgetallen (die bij de bovenste som bovendien verschillend zijn) :$$ 3~primes \left[ \begin{matrix} &&\mathbf{2}&+&\mathbf{3}&+&\mathbf{7}\\ \\ &2&+&5&+&5 \end{matrix} \right. $$ | 12.6 |
\(12\) is gelijk aan \(4\) maal de som van zijn cijfers : \(12=4*(1+2)\). Andere getallen met deze eigenschap zijn veelvouden van \(12\), namelijk \(24,36\) en \(48~~\) ( ) (OEIS A005349 - Harshad getallen) Zie ook bij | 12.7 |
|
\(12=3*4~~\) (vier opeenvolgende cijfers) (Fun With Num3ers) Dit patroon doet zich enkel nog voor bij \(56=7*8~~\) | 12.8 |
| De som van twee priemtweelingen (groter dan \(3\)) is deelbaar door \(12\). Bvb. de priemtweelingen \(5867\) en \(5869\) : \(5867+5869=11736=12*978\) | 12.9 |
| \(12\) is ook een deler van het product van drie opeenvolgende getallen \((A-1)*A*(A+1)\) op voorwaarde dat \(A\) (= het middelste getal van de drie) oneven is (men heeft dan het product van een even, een oneven en nog een even getal). Bvb. met \(A=29\) komt er : \(28*29*30=24360=12*2030\) | 12.10 |
| \(12!+34567\) is een priemgetal (\(479036167\)) | 12.11 |
\(12\) is één van de \(8\) getallen van \(2\) verschillende cijfers dat gelijk is aan een ééncijferveelvoud van het cijfer van de eenheden : \(12=6*2\). De andere getallen zie bij | 12.12 |
| \(12\) kan niet geschreven worden als som van verschillende driehoeksgetallen. Zie voor meer toelichting bij | 12.13 |
| Als men van \(12\) het product maakt van al zijn delers dan krijgt men een macht van \(12\) : \(1*2*3*4*6*12=\) \(1728=12^3\). Soortgelijk patroon vindt men bij andere veelvouden van \(12\) die geen kwadraat zijn (uiteraard zal de exponent hoger zijn dan \(3\); de exponent is immers gelijk aan de helft van het aantal delers). Zie ook bij | 12.14 |
| Alle pare machten van \(12\), verminderd met \(1\), zijn deelbaar door \(143\) : bvb. \(12^4=20736\) en \(20735=143*145\) Alle onpare machten van \(12\), verminderd met \(1\) , zijn deelbaar door \(11\) : bvb. \(12^3=1728\) en \(1727=11*157\) De som van de cijfers van een willekeurige macht van \(12\) (met uitzondering van \(12^1\)) is een veelvoud van \(9\), bvb. \(12^5=248832~~\) en \(~~2+4+8+8+3+2=27=9*3\) | 12.15 |
\(12^2\mathbf{\color{blue}{\;=\;}}10^3-8^3-7^3-1^3\mathbf{\color{blue}{\;=\;}}10^3-9^3-7^3+6^3\). \(12^2=1*2*3*4*6\) (de \(5\) ontbreekt) = \(6!/5\) \(12^2=144\) en het omgekeerde is ook waar : \(21^2=441\) \(12^2+33^2=1233\). Zie ook bij \(12^3=9^3+10^3-1^3\) \(12^3=6^3+8^3+10^3\) (derdemachten van opeenvolgende pare getallen) | 12.16 |
\(12=(1+2)+(1^3+2^3)\) ( Er zijn \(6\) getallen met deze eigenschap : getal = som van de cijfers plus som van \(\qquad\,\) de derdemachten van de cijfers; die getallen zijn : \(12,30,666,870,960\) en \(1998\) ) (OEIS A065138) | 12.17 |
| \(12^5\mathbf{\color{blue}{\;=\;}}4^5+5^5+6^5+7^5+9^5+11^5\mathbf{\color{blue}{\;=\;}}248832\) is de kleinste vijfdemacht die de som van zes positieve vijfdemachten is. | 12.18 |
De volgende producten zijn symmetrisch ten opzichte van het gelijkheidsteken : \begin{align} 12*42&=24*21\to504\\ 12*63&=36*21\to736\\ 12*84&=48*21\to1008 \end{align} | 12.19 |
| \(12*23=276\gets\) leest van rechts naar links \(\to672=32*21\) | 12.20 |
| Palindromische vormen (met leidende nul) : \(12*\underline{0495=5940}\quad\) en \(\quad\underline{012*210}=\underline{120*021}\to2520\) | 12.21 |
| Het omgekeerde van \(12\) is \(21\); het omgekeerde van \(24\,(=2*12)\) is \(42\,(=2*21)\). Hetzelfde patroon heeft men met \(36\;(63)\) en \(48\;(84)\). | 12.22 |
| Alle cijfers van \(1\) tot \(9\) komen voor in \(12*483=5796\quad\) (Trouwens men heeft ook \(5796=42*183\)) | 12.23 |
(multigrades) \(12\to62\to\) \begin{align} 1^1+5^1+6^1&=2^1+3^1+7^1\\ 1^2+5^2+6^2&=2^2+3^2+7^2 \end{align} | 12.24 |
| \(12\) schrijven met behulp van de cijfers \(1,2,3\) en \(4\) : \(\quad(4-3)*12~~=~~1*2*3*\sqrt4~~=~~4^2-3-1~~=~~3^2+1+4-2~~=~~(2-1)*3*4~~=~~\) \(\quad2*(4+3-1)~~=~~2^4-1-3~~=~~(3*4)/(2-1)~~=~~4!/(3-2+1)\) Zie ook bij | 12.25 |
| \(12\) is het kleinste overvloedige getal (Eng: Abundant number) d.w.z. een getal dat kleiner is dan de som van zijn delers inclusief \(1\) en exclusief zichzelf. Zie ook bij (OEIS A005101) Kortom \(12 \to1+2+3+4+6=16\) en \(12\lt16\). | 12.26 |
| Er zijn \(12\) pentomino's (figuren bestaande uit vijf vierkanten die aan één of meer zijden samengevoegd zijn). Deze kunnen een totaal oppervlak van \(12*5=60\) eenheden bedekken, bvb. een rechthoek van \(3*20;4*15;5*12\) of \(6*10\). Tal van andere mogelijkheden bestaan. Zie illustratie bij en ook | 12.27 |
Twee driehoeken met zijden \((5;5;6)\) en \((5;5;8)\) hebben beide als oppervlakte een waarde van \(12\). Driehoeken met gehele zijden en waarvan de oppervlakte een geheel getal is, heten driehoeken van HERON (of HERO). | 12.28 |
| Er zijn vier rechthoekige driehoeken met gehele zijden en \(12\) als één van de zijden : \((5;12;13),(9;12;15),(12;16;20),(12;35;37)\) | 12.29 |
| Enkele getalpiramides \begin{align} 3*4&=12\\ 33*34&=1122\\ 333*334&=111222\\ 3333*3334&=11112222\\ \cdots&=\cdots \end{align} \begin{align} 1*9+2&=11\\ 12*9+3&=111\\ 123*9+4&=1111\\ 1234*9+5&=11111\\ 12345*9+6&=111111\\ 123456*9+7&=1111111\\ 1234567*9+8&=11111111\\ \cdots&=\cdots \end{align} \begin{align} 35^2&=1225\\ 335^2&=112225\\ 3335^2&=11122225\\ 33335^2&=1111222225\\ 333335^2&=111112222225\\ 3333335^2&=11111122222225\\ \cdots&=\cdots \end{align} | 12.30 |
| De som van de kwadraten van drie opeenvolgende oneven getallen, plus \(1\), is een veelvoud van \(12\). Men heeft in formulevorm : \((2n-1)^2+(2n+1)^2+(2n+3)^2=12n^2+12n+12=12*(n^2+n+1)\) | 12.31 |
| IETS SPECIAALS
Het getal \(12\) heeft \(6\) delers : \(1;2;3;4;6;12\). Het getal \(6\) is een perfect getal. De som Dit reuzengetal bestaat in feite uit een macht van \(2\), vermenigvuldigd met een aantal MERSENNE-priemgetallen. | 12.32 |
| MERKWAARDIG
Met de cijfers \(0,1\) en \(2\) voor de grondtallen en de cijfers \(0,1\) en \(4\) voor de kwadraten | 12.33 |
| Men moet \(12\) tot minimaal de \(588\)ste macht verheffen opdat in de decimale expansie exact \(12\) \(12\)'s verschijnen. Noteer, voor wat het waard is, dat \(588\) deelbaar is door \(12\to588/12=49\). Terloops : \(12\)\(^{588}\) is \(635\) cijfers lang. Getallen \(n\) waarbij het cijfer \(1\) niet voorkomt in de decimale expansie van \(n,n^2\) als \(n^3\) : \(588\to345744\to203297472~~\) en \(~~635\to403225\to256047875~~~~\) (OEIS A255357) | 12.34 |
Als som met de vier operatoren \(+-*\;/\) | 12.35 |
| \(12\) als resultaat met breuken waarin de cijfers van \(1\) tot \(9\) exact één keer voorkomen : (\(4\) oplossingen) \(45792/3816=73548/6129=89532/7461=91584/7632=12\) \(12\) als resultaat met breuken waarin de cijfers van \(0\) tot \(9\) exact één keer voorkomen : (\(1\) oplossing) \(107352/8946=12\) | 12.36 |
| Een hexaëder (kubus) heeft \(12\) ribben. Een icosaëder (twintigvlak) heeft \(12\) hoekpunten. \(12\) pentagons (vijfhoeken) zijn er nodig om een regelmatige dodecaëder (twaalfvlak) te vormen. 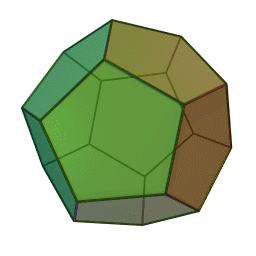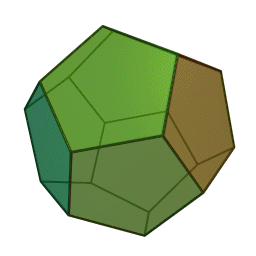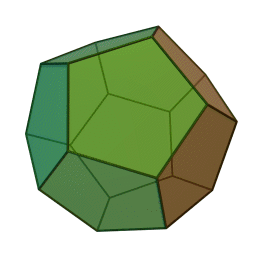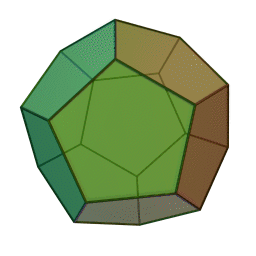 | 12.37 |
\(12!-1\) is een priemgetal \((=479001599)\), de vijfde in zijn soort \((k!-1)~~\) (OEIS A002982) | 12.38 |
Alle getallen van \(1\) tot \(12\) worden gebruikt, hetzij als grondtal hetzij als exponent, in deze gelijkheden van producten van machten. Vele andere combinaties zijn mogelijk. Verdeelsleutel \([1-5]\) levert geen oplossingen. Verdeelsleutel \([2-4]\) levert \(61\) zuivere oplossingen. Verdeelsleutel \([3-3]\) heeft er netto \(114\). \begin{align} 2^{10}*12^{11}&\mathbf{\color{blue}{\;=\;}}3^1*4^7*8^6*9^5\\ 2^{11}*3^7*4^{12}&\mathbf{\color{blue}{\;=\;}}6^5*8^{10}*9^1 \end{align} | 12.39 |
\(12\) als som van zes getallen (op een cirkel geplaatst) die één voor één het product zijn van hun buurgetallen \(12=6+2+{\Large\frac{1}{3}}+{\Large\frac{1}{6}}+{\Large\frac{1}{2}}+3\) | 12.40 |
\(10^2+11^2+{\color{blue}{12^2}}=13^2+14^2=\) | 12.41 |
\(\begin{align}12\mathbf{\color{blue}{\;=\;}}\left({\frac{19}{39}}\right)^3+\left({\frac{89}{39}}\right)^3\end{align}\) (Integral Sum of Two Rational Cubes) (OEIS A020898) (OEIS A228499) (Links uit OEIS A060838) \((x^3+y^3)/z^3=n~\to~\) [x waarde] (OEIS A190356) [y waarde] (OEIS A190580) [z waarde] (OEIS A190581) Kleinste positieve oplossingen \(~\to~\) [x waarde] (OEIS A254326) [y waarde] (OEIS A254324) | 12.42 |
\(2\)\(^{12}\)\(\,+\,3\) is een priemgetal \((=4099)\), de zevende in zijn soort \((2^k+3)~~\) (OEIS A057732) \(2\)\(^{12}\)\(\,-\,3\) is een priemgetal \((=4093)\), de zevende in zijn soort \((2^k-3)~~\) (OEIS A050414) | 12.43 |
Som der reciproken van partitiegetallen van \(12\) levert nooit \(1\) op. Bijgevolg ook geen partities met unieke termen. | 12.44 |
○–○–○ \(12^2=144~~\) en \(~~(-1+4)*4=12\)\(12^3=1728~~\) en \(~~-1+7-2+8=12\) \(12^4=20736~~\) en \(~~2+0+7-3+6=12\) \(12^5=248832~~\) en \(~~2+4+8/8+3+2=12\) \(12^6=2985984~~\) en \(~~2*9-8+5+9-8-4=12\) \(12^7=35831808~~\) en \(~~3+5-8-3-1+8+0+8=12\) \(12^8=429981696~~\) en \(~~4+2+9-9+8+1-6+9-6=12\) \(12^9=5159780352~~\) en \(~~-5+15-9-7+8+0+3+5+2=12\) \(12^{10}=61917364224~~\) en \(~~619+1+7+3-642+24=12\) \(12^{11}=743008370688~~\) en \(~~74+30+0-8+3+7+0-6-88=12\) \(12^{12}=8916100448256~~\) en \(~~891+6-10+0-44-825-6=12\) \(12^{13}=106993205379072~~\) en \(~~10+6-9-9-3+2+0+5+3+7-9+0+7+2=12\) \(12^{14}=1283918464548864~~\) en \(~~12-8-3+9+1+8-46+4+5+4+8+8+6+4=12\) \(12^{15}=15407021574586368~~\) en \(~~15+4+0-7+0-2+1-5+74+5-8+6-3-68=12\) \(12^{16}=184884258895036416~~\) en \(~~18+48-8+4+2-58+89-50-36-4+1+6=12\) \(12^{17}=2218611106740436992~~\) en \(~~22+1+86+1-110+6+7+4+0-4+3-6+9-9+2=12\) \(12^{18}=26623333280885243904~~\) en \(~~266-233-33-2+8+0+88+5-2+4-3-90+4=12\) \(12^{19}=319479999370622926848~~\) en \(~~31+9-4+7+99-99-37+0+62+2-92-6-8+48=12\) \(12^{20}=3833759992447475122176~~\) en \(~~38-33+75-99+92-44+74-75-12-2-1-7+6=12\) | 12.45 |
Expressie met tweemaal de cijfers uit het getal \(12\) enkel met operatoren \(+,-,*,/,(),\)^^\(\) | 12.46 |
| \(12\) is de som van de termen van een priemtweelingenpaar \(5+7\) en \(12^2=144\) idem dito namelijk \(71+73~~\) (OEIS A213784) | 12.47 |
Som Der Cijfers (\(sdc\)) van \(k^{\large{12}}\) is gelijk aan het grondtal \(k\). De triviale oplossingen \(0\) en \(1\) negerend vinden we : \(\qquad\qquad~sdc\left(108^{\large{12}}\right)=108~~\to\) Unieke oplossing voor \(k\gt1\). Noteer dat \(108=12*(1+0+8)\) | 12.48 |
| Het kwadraat van \(12\) kan uitgedrukt worden als een som van verschillende faculteiten. \(12^2=144=4!+5!~~\) (OEIS A014597) In totaal zijn er maar \(15\) getallen van deze soort gekend. | 12.49 |
| Exponent \(12\) heeft geen groter grondtal dan \(4\) zodat de decimale expansie van deze macht geen cijfers bevat uit het grondtal\(~~~~\to~~~~4^{12}=16777216\) (OEIS A113951) | 12.50 |
\(12\) is een getal van de vorm \(2\)\(^k\)\(+k\)\(^3\), de derde in zijn soort. Reken uit met de waarde \(k=2~~\). (OEIS A097339) | 12.51 |
Als expressie met enkelcijferige toepassing, resp. van \(1\) tot \(9~~\) (met dank aan Inder. J. Taneja). | 12.52 |
Met de cijfers van \(1\) tot \(9\) in stijgende en dalende volgorde (met dank aan Inder. J. Taneja) : | 12.53 |
Expressie van \(n\) enkel gebruik makend van faculteiten, vierkantswortels en afrondingen. In Pari/GP code : \(12~=~\)floor(sqrt(sqrt(sqrt(12!)))) \(\qquad\qquad12={\huge\lfloor}\sqrt{\sqrt{\sqrt{12!}}}{\huge\rfloor}\) | 12.54 |
\({\Large\frac{400}{33}}=12,1212121212121212121212\ldots\) | 12.55 |
\({\Large\frac{1}{12^2}=\frac{1}{15^2}+\frac{1}{20^2}}~~~~\) (kleinste gehele getallen van de reciproke Pythagoras vergelijking) | 12.56 |
Het omgekeerde van \(4^{12}\) is een priemgetal \(\to{61277761}\) Pari/GP code : isprime(fromdigits(Vecrev(digits(4^12))))\(\to1=\) true | 12.57 |
Het omgekeerde van \(7^{12}\) is een priemgetal \(\to{10278214831}\) Pari/GP code : isprime(fromdigits(Vecrev(digits(7^12))))\(\to1=\) true | 12.58 |
| Het kleinste getal dat exact \(12\) delers heeft is \(60=2^2*3*5\). (OEIS A005179) | 12.59 |
| \(12\) is de omtrek van een rechthoekige driehoek met gehele zijden \((3;4;5)\). | 12.60 |
| \(12\) is het eerste getal zodat \({\large\sigma}(x)=k\) exact twee oplossingen heeft \(~~({\large\sigma}(x)\) of \(Sigma(x)\) is de som der delers). Hier zijn die twee oplossingen : \(x\to{\large\sigma}(6),~{\large\sigma}(11)\) Andere waarden van \(k\) zie (OEIS A201915) en (OEIS A007368) | 12.61 |
| \(12\) is het aantal partities van \(11\) met verschillende termen. (OEIS A000009) Onderstaande Pari/GP code zet ze allemaal op een rijtje. q=partitions(11); c=0; for(i=1,#q, z=q[i]; f=1; for(j=1,#z-1, if(z[j]==z[j+1], f*=0));if(f, c++; print(c," ",q[i]))) | 12.62 |
(zes multigrades) \(12\to12^5\to\) \begin{aligned} 12^1&=27^1+106^1-122^1-228^1+229^1\\ 12^5&=27^5+106^5-122^5-228^5+229^5\\ \\ 12^1&=156^1+224^1-388^1-524^1+544^1\\ 12^5&=156^5+224^5-388^5-524^5+544^5\\ \\ 12^1&=-123^1-213^1+351^1+753^1-756^1\\ 12^5&=-123^5-213^5+351^5+753^5-756^5\\ \\ 12^1&=-101^1-433^1+571^1+764^1-789^1\\ 12^5&=-101^5-433^5+571^5+764^5-789^5\\ \\ 12^1&=-83^1-304^1+403^1+794^1-798^1\\ 12^5&=-83^5-304^5+403^5+794^5-798^5\\ \\ 12^1&=160^1+672^1-860^1-1116^1+1156^1\\ 12^5&=160^5+672^5-860^5-1116^5+1156^5\\ \end{aligned} | 12.63 |
| \(12de\) machten van twee getallen schijnen de laatste stelling van Fermat te weerleggen. Doe de volgende berekening op een normaal wetenschappelijk rekenmachientje : \(\root{\raise3pt{\large12}}\of{1782^{12}+1841^{12}}\) De uitkomst geeft een geheel getal weer namelijk \(1922\) ! Helaas hebben we hier te maken met een afrondingsfout die ons een illusie geeft van wat er werkelijk gebeurt voorbij de komma. Gebruikmakend van een computer met een voldoende 'multiple precision' capaciteit (dus zonder afrondingen) zien we \(\root{\raise3pt{\large12}}\of{1782^{12}+1841^{12}}=1921.9999999558672254029113283702950729\ldots\) en dat is geen geheel getal. De stelling van Fermat blijft overeind ! Een gelijkaardig zgn. tegenvoorbeeld verscheen in de Amerikaanse serie 'The Simpsons' waar Homer voor een bord staat met de volgende formule \(~~3987^{12}+4365^{12}=4472^{12}\) Zonder afronding hebben we hier eigenlijk \(~~3987^{12}+4365^{12}=(4472.00000000705929073821352924\ldots)^{12}\) | 12.64 |
\(12\) is het product van twee opeenvolgende getallen (pronic) \(=3*4~~\) (OEIS A002378) | 12.65 |
Taxicab-getallen zijn te schrijven zijn als de som van \(2\) positieve derdemachten op \(n\) verschillende wijzen. Nemen we \(~n=2~\) dan komt ons getal \(12\) ten tonele vermits \(1729\mathbf{\color{green}{\;=\;}}1^3+{\color{blue}{12}}^3\mathbf{\color{green}{\;=\;}}9^3+10^3\) (OEIS A003824) (OEIS A016078) (OEIS A018786) (OEIS A046881) (OEIS A230562) (OEIS A343077) | 12.66 |
| De som van de eerste \(12\) priemgetallen is een priemgetal (OEIS A013916) (OEIS A013918). Pari/GP code : sum(i=1,12,prime(i)) \(~~isprime(197)~~\to~~1~(true)\) | 12.67 |
\(12\mathbf{\color{blue}{\;=\;}}13^2+78^2-79^2\mathbf{\color{blue}{\;=\;}}13+78-79\) \(12\mathbf{\color{blue}{\;=\;}}14^2+45^2-47^2\mathbf{\color{blue}{\;=\;}}14+45-47\) \(12\mathbf{\color{blue}{\;=\;}}15^2+34^2-37^2\mathbf{\color{blue}{\;=\;}}15+34-37\) \(12\mathbf{\color{blue}{\;=\;}}18^2+23^2-29^2\mathbf{\color{blue}{\;=\;}}18+23-29\) | 12.68 |