\(10\mathbf{\color{blue}{\;=\;}}1+2+3+4\) (som van opeenvolgende gehele getallen) \(10\mathbf{\color{blue}{\;=\;}}4+6\) (som van opeenvolgende pare getallen) \(10\mathbf{\color{blue}{\;=\;}}1+3+6\mathbf{\color{blue}{\;=\;}}D(1)+D(2)+D(3)\mathbf{\color{blue}{\;=\;}}D(4)~~\) \(\qquad\;\,\)(som van driehoeksgetallen en bovendien zelf een driehoeksgetal) (OEIS A222716) \(10\mathbf{\color{blue}{\;=\;}}{\color{red}{2}}+3+{\color{red}{5}}\) (som van opeenvolgende priemgetallen) (som van opeenvolgende Fibonaccigetallen) \(\qquad\;\,\)en ook \(10={\color{red}{2}}*{\color{red}{5}}\) (eerste en laatste priemgetal uit de vorige rij) (OEIS A055233) \(10\mathbf{\color{blue}{\;=\;}}3^2+1\mathbf{\color{blue}{\;=\;}}2^3+2\) \(10\mathbf{\color{blue}{\;=\;}}4^2-3^2+2^2-1^2\) \(10\mathbf{\color{blue}{\;=\;}}1^2+3^2\mathbf{\color{blue}{\;=\;}}1^2+1^2+2^2+2^2\mathbf{\color{blue}{\;=\;}}((0;0;1;3)\,(1;1;2;2))\lower2pt{\Large{\color{teal}{➋}}}\to\{\#2\}\) \(10\mathbf{\color{blue}{\;=\;}}\bbox[#f4f4f4,3px,border:1px solid]{1^3+1^3+2^3}\mathbf{\color{blue}{\;=\;}}\)(som van drie positieve derdemachten)\(\mathbf{\color{blue}{\;=\;}}(0;0;0;0;0;0;1;1;2)\lower2pt{\Large{\color{teal}{➌}}}\to\{\#1\}\) \(10\mathbf{\color{blue}{\;=\;}}\Large\frac{\sqrt{10^3\,-\,10^2}}{\lfloor\sqrt{10}\,\rfloor}~~\)(OEIS A087279) \(10\mathbf{\color{blue}{\;=\;}}13^3-3^7~~\) (enige oplossing met limieten grondtal \(9999\) en exponent \(19\) ) | 10.1 | ||
\(10\mathbf{\color{blue}{\;=\;}}\)(som van drie derdemachten) \(\qquad\;\,10\) oplossingen bekend \(\qquad\;\,\)References Sum of Three Cubes \(10\mathbf{\color{blue}{\;=\;}}\)(som van vijf vijfdemachten) \(\qquad\;\,\)(fully searched up to \(z=1000)\) \(\qquad\;\,\bbox[3px,border:1px blue solid]{(-1)^5+(-1)^5+13^5+16^5+(-17)^5}\mathbf{\color{blue}{\;=\;}}\to~~\)Noteer dat\(~~-1-1+13+16-17\mathbf{\color{blue}{\;=\;}}10\) | 10.2 | ||
\(10^2\mathbf{\color{blue}{\;=\;}}\to\) als som of verschil van twee machten zie bij paginagetal \(100\) \(10^3\mathbf{\color{blue}{\;=\;}}\to\) als som of verschil van twee machten zie bij paginagetal \(1000\) | 10.3 | ||
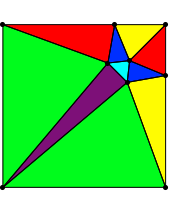
Een vierkant kan verdeeld worden in \(10\) scherphoekige, gelijkbenige driehoeken. De dubbele voorwaarde
| 10.4 | ||
| \(10\) als resultaat met breuken waarin de cijfers van \(1\) tot \(9\) of van \(0\) tot \(9\) exact één keer voorkomen : (\(geen\) oplossingen → ook niet voor de veelvouden van \(10\)). | 10.5 | ||
\(10=0!+1!+2!+3!\) \(10!=6!*7!~~\) (uniek patroon met twee opeenvolgende faculteiten) \(10!=1!*3!*5!*7!~~\) of \(~~10!=3!*5!*7!\) \(10\mathbf{\color{blue}{\;=\;}}1+1+1+2+5\mathbf{\color{blue}{\;=\;}}1*1*1*2*5\) | 10.6 | ||
| Het tientallig stelsel (het decimale stelsel of het getalstelsel met basis \(10\)) is in het dagelijkse leven het gebruikelijkst. Computers rekenen met het tweetallig (of binaire) stelsel of het zestientallige (of hexadecimale) stelsel. De oorsprong van het tientallig stelsel ligt in het feit dat we \(10\) vingers hebben. | 10.7 | ||
\(10^2=1^2+3^2+4^2+5^2+7^2\) \(10^2=14^2+13^2-12^2-11^2~~~~\) of \(~~~~10^2+11^2+12^2=13^2+14^2\) \(10^2=1^3+2^3+3^3+4^3\) | 10.8 | ||
| \(10\) is het kleinste getal dat op meer dan één wijze (in dit geval op twee wijzen) kan worden geschreven als de som van twee priemgetallen (bovendien zijn alle getallen oneven) : $$ 2\;odd\;primes \left[ \begin{matrix} &3&+&7\\ \\ &5&+&5 \end{matrix} \right. $$ \(10\) als som van drie, vier en vijf priemgetallen :$$ 3,4\;\&\;5\;primes \left[ \begin{matrix} &&\mathbf{2}&+&\mathbf{3}&+&\mathbf{5}\\ &2&+&2&+&3&+&3\\ &2&+&2&+&2&+&2&+&2 \end{matrix} \right. $$ | 10.9 | ||
Negen getallen zijn gelijk aan \(10\) maal de som van hun cijfers \(10,20,30,40,50,60,70,80,90\) | 10.10 | ||
| \(10-1\mathbf{\color{blue}{\;=\;}}9\mathbf{\color{blue}{\;=\;}}3^2~~\) en de helft \(~~10/2-1\mathbf{\color{blue}{\;=\;}}4\mathbf{\color{blue}{\;=\;}}2^2\) | 10.11 | ||
| \(10=2*5\) en de lijst van priemgetallen van \(2\) tot \(5\) is \(2,3,5\). Bovendien is \(2+3+5=10\). Het volgende getal met dezelfde eigenschap is \(39\) (zie ) en (OEIS A055514) | 10.12 | ||
Elke macht van \(10\) kan worden geschreven als het product \(10*10*10*\dots\), bvb. \(10^4=10*10*10*10\). | 10.13 | ||
| Als men de letters van “TIEN” vormt met lucifers, dan heeft men precies \(10\) lucifers nodig. Dit gebeurt bij geen enkel ander getal. | 10.14 | ||
| Een ruwe benadering van \(\Large{\pi}\) wordt gegeven door \(\sqrt{10}=3,16\) (de werkelijke waarde van \(\Large{\pi}\) is \(3,141562\ldots\)) | 10.15 | ||
| \(10\) is zowel driehoeksgetal \((10=1+2+3+4)\) als viervlaksgetal \((10=1+3+6)\). Dat betekent dat men \(10\) ballen kan schikken zowel tweedimensionaal in een driehoek met zijde \(4\), als driedimensionaal in een piramide met onderste laag een gelijkzijdige driehoek van \(6\) ballen, hierop een driehoek met \(3\) ballen en bovenop de laatste bal. Het volgende getal met die eigenschap is \(120\). Zie ook aldaar. (OEIS A027568) | 10.16 | ||
| \(10\) schrijven met behulp van de cijfers \(1,2,3\) en \(4\) : \(\quad1+2+3+4~~=~~(3!+4!)/(1+2)~~=~~(2*4)+(3-1)~~=~~3^2+\sqrt4-1~~=~~(3*4-2)*1\) | 10.17 | ||
| Er zijn twee rechthoekige driehoeken met gehele zijden en \(10\) als één van de zijden : \((6;8;10),(10;24;26)\) | 10.18 | ||
| Elk even getal, hier geïllustreerd met het getal \(10\), is gelijk aan het verschil van twee opeenvolgende kwadraten verminderd met \(1\). Het kleinste kwadraat is dan de helft van het initiële even getal. \(10=6^2-5^2-1\quad\) en \(\quad5=\Large{10\over2}\) | 10.19 | ||
| EEN PUZZEL
\(\bbox[3px,border:1px solid blue]{\;Opgave\;}\) | 10.20 | ||
| EEN PUZZEL
\(\bbox[3px,border:1px solid blue]{\;Opgave\;}\) (met o.a. dank aan Inder. J. Taneja) | 10.21 | ||
| Verschillende wijzen om \(10\) te maken met vier achten. \(\qquad\qquad10\mathbf{\color{blue}{\;=\;}}\sqrt{8*8}+\sqrt{\sqrt{8+8}}\) \(\qquad\qquad10\mathbf{\color{blue}{\;=\;}}8,8/,88\) \(\qquad\qquad10\mathbf{\color{blue}{\;=\;}}88/8,8\) \(\qquad\qquad10\mathbf{\color{blue}{\;=\;}}(8+8-8)/,8\) \(\qquad\qquad10\mathbf{\color{blue}{\;=\;}}8/(,8+8-8)\) \(\qquad\qquad10\mathbf{\color{blue}{\;=\;}}\sqrt{88/,88}\) \(\qquad\qquad10\mathbf{\color{blue}{\;=\;}}(8+8)/(,8+,8)\) \(\qquad\qquad10\mathbf{\color{blue}{\;=\;}}8+8/\sqrt{8+8}\) \(\qquad\qquad10\mathbf{\color{blue}{\;=\;}}(8+8)/8+8\) \(\qquad\qquad10\mathbf{\color{blue}{\;=\;}}8/8*8/,8\) \(\qquad\qquad10\mathbf{\color{blue}{\;=\;}}8*(8-8)!/,8\) \(\qquad\qquad10\mathbf{\color{blue}{\;=\;}}(88-8)/8\) | 10.22 | ||
| \(10\) is een semipriemgetal (dat is een samengesteld getal dat gelijk is aan het product van twee gelijke of verschillende priemdelers). Voor \(10\) zijn dat de priemdelers \(2\) en \(5\). Het unieke is dat zowel de som als het verschil van beide priemdelers van \(10\) telkens priemgetallen zijn : \(5+2=7\) en \(5-2=3\). Dit geldt enkel voor het getal \(10\). | 10.23 | ||
\(10*(A+B)=A*B\) heeft vijf oplossingen in gehele getallen : | 10.24 | ||
| Het kleinste gemene veelvoud van all positieve gehele getallen van \(1\) tot en met \(10\) is \(2520\) \((5*7*8*9~\) of \(~2^3*3^2*5*7)\). | 10.25 | ||
Er is slechts \(1\) getal van tien cijfers dat gelijk is aan de som van de \(tiende\) macht van zijn cijfers : \(4679307774=4\)\(^{10}\)\(\,+\,6\)\(^{10}\)\(\,+\,7\)\(^{10}\)\(\,+\,9\)\(^{10}\)\(\,+\,3\)\(^{10}\)\(\,+\,0\)\(^{10}\)\(\,+\,7\)\(^{10}\)\(\,+\,7\)\(^{10}\)\(\,+\,7\)\(^{10}\)\(\,+\,4\)\(^{10}\) | 10.26 | ||
Alle getallen van \(1\) tot \(10\) worden gebruikt, hetzij als grondtal hetzij als exponent, in deze gelijkheden van producten van machten. Verdeelsleutel \([1-4]\) levert geen oplossingen. Verdeelsleutel \([2-3]\) levert \(2\) zuivere oplossingen. Hier zijn ze : \begin{align} 3^5*8^7&\mathbf{\color{blue}{\;=\;}}4^{10}*6^1*9^2\\ 6^{10}*8^1&\mathbf{\color{blue}{\;=\;}}2^7*4^3*9^5 \end{align} | 10.27 | ||
Voor \(n=10~~\) geldt \(~~{\large\sigma}(n)={\large\sigma}(n+7) ~~\to~~ {\large\sigma}(10)={\large\sigma}(17)=18~~~~({\large\sigma}\) of 'sigma' staat voor som der delers) \(10\) is de eerste oplossing uit (OEIS A015867) | 10.28 | ||
In deze Numberphile YouTube Video A Video about the Number 10 - Numberphile is James Grime op zoek naar een | 10.29 | ||
Som der reciproken van partitiegetallen van \(10\) is \(1\) op één wijze. Deze partitie heeft evenwel geen unieke termen. \((1)~~10=2+4+4~~\) en \(~~1={\Large\frac{1}{2}}+{\Large\frac{1}{4}}+{\Large\frac{1}{4}}\) | 10.30 | ||
\(1+2+3+4+5+6+7+8+9+{\color{blue}{10}}=55=1^2+2^2+3^2+4^2+5^2\) | 10.31 | ||
\({\color{blue}{10^2}}+11^2+12^2=13^2+14^2={\color{tomato}{365}}\) Gelijkheid van twee sommen met doorlopend opeenvolgende kwadraten. De eerste term van de linkersom is (OEIS A014105). De eerste term van de rechtersom is (OEIS A001804). \(2*m-1=2*13-1=25=5^2\) is een perfect kwadraat. Het verschil \(13-10=3\) geeft het aantal termen weer van de linkersom. En ééntje minder in de rechtersom. | 10.32 | ||
\(10!+10+1\) is een priemgetal, de zesde in zijn soort \((k!+k+1)~~\) (OEIS A073308) | 10.33 | ||
\(2\)\(^{10}\)\(\,-\,3\) is een priemgetal \((=1021)\), de zesde in zijn soort \((2^k-3)~~\) (OEIS A050414) | 10.34 | ||
Som Der Cijfers (\(sdc\)) van \(k^{\large{10}}\) is gelijk aan het grondtal \(k\). De triviale oplossingen \(0\) en \(1\) negerend vinden we : \(\qquad\qquad~sdc\left(82^{\large{10}}\right)=82\qquad\qquad~sdc\left(85^{\large{10}}\right)=85\quad\qquad\qquad~sdc\left(94^{\large{10}}\right)=94\) \(\qquad\qquad~sdc\left(97^{\large{10}}\right)=97\qquad\qquad~sdc\left(106^{\large{10}}\right)=106\qquad\qquad~sdc\left(117^{\large{10}}\right)=117\) | 10.35 | ||
Expressies met tweemaal de cijfers uit het getal \(10\) | 10.36 | ||
Expressie van \(n\) enkel gebruik makend van faculteiten, vierkantswortels en afrondingen. In Pari/GP code \(10~=~\)floor(sqrt(prod(j=1,floor(sqrt(sqrt(prod(i=1,10/2,i*2))))/2,2*j+1))) \(\qquad\qquad10={\Huge\lfloor}\sqrt{{\huge\lfloor}\sqrt{\sqrt{10!!}}{\huge\rfloor}!!}{\Huge\rfloor}\) | 10.37 | ||
| Exponent \(10\) heeft geen groter grondtal dan \(18\) zodat de decimale expansie van deze macht geen cijfers bevat uit het grondtal\(~~~~\to~~~~18^{10}=3570467226624\) (OEIS A113951) | 10.38 | ||
| 10.39 | ||
| \(10\) is de som van de eerste \(2\) semipriemgetallen \((4+6)\). (OEIS A062198) | 10.40 | ||
Het omgekeerde van \(2^{10}\) is een priemgetal \(\to{4201}\) Pari/GP code : isprime(fromdigits(Vecrev(digits(2^10))))\(\to1=\) true | 10.41 | ||
| \(10^3=19^3+24^3-27^3\) | 10.42 | ||
| Schikking met oplopende machten van \(10\) in piramidevorm :
\begin{align} 10^0&=1\\ 10^0+10^1&=11\\ 10^0+10^1+10^2&=111\\ 10^0+10^1+10^2+10^3&=1111\\ 10^0+10^1+10^2+10^3+10^4&=11111\\ 10^0+10^1+10^2+10^3+10^4+10^5&=111111\\ 10^0+10^1+10^2+10^3+10^4+10^5+10^6&=1111111 \end{align} | 10.43 | ||
| Het kleinste getal dat exact \(10\) delers heeft is \(48=2^4*3\). (OEIS A005179) | 10.44 | ||
| \(10\) is het aantal partities van \(10\) met verschillende termen. (OEIS A000009) Onderstaande Pari/GP code zet ze allemaal op een rijtje. q=partitions(10); c=0; for(i=1,#q, z=q[i]; f=1; for(j=1,#z-1, if(z[j]==z[j+1], f*=0));if(f, c++; print(c," ",q[i]))) | 10.45 | ||
Met de cijfers van \(1\) tot \(9\) in stijgende en dalende volgorde (met o.a. dank aan Inder. J. Taneja) : | 10.46 | ||
(twee multigrades) \(10\to10^5\to\) \begin{aligned} 10^1&=98^1+531^1-636^1-915^1+932^1\\ 10^5&=98^5+531^5-636^5-915^5+932^5\\ \\ 10^1&=-262^1-1218^1+1610^1+1858^1-1978^1\\ 10^5&=-262^5-1218^5+1610^5+1858^5-1978^5\\ \end{aligned} | 10.47 | ||
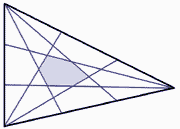
| \(10\) is het aantal snijpunten (Eng. nodes) dat ontstaat wanneer de diagonalen van een regelmatige vijfhoek worden getekend. (OEIS A007569) | 10.48 | ||
\(10\) kan op velerlei wijzen uitgedrukt worden als een breuk met als teller en noemer telkens een product van \(2\) pandigitale getallen. Hier is alvast één voorbeeld : \(10=\Large{\frac{4093827156\;*\;2561839740}{1023456789\;*\;1024735896}}\) | 10.49 | ||
Taxicab-getallen zijn te schrijven zijn als de som van \(2\) positieve derdemachten op \(n\) verschillende wijzen. Nemen we \(~n=2~\) dan komt ons getal \(10\) ten tonele vermits \(1729\mathbf{\color{green}{\;=\;}}1^3+12^3\mathbf{\color{green}{\;=\;}}9^3+{\color{blue}{10}}^3\) (OEIS A003824) (OEIS A016078) (OEIS A018786) (OEIS A046881) (OEIS A230562) (OEIS A343077) | 10.50 | ||
| Er zijn \(10\) semipriemgetallen \(n\) kleiner dan honderd zodanig dat \(n+1\) ook een semipriemgetal is. Pari/GP code : cnt=0; for(n=1, 10^2, if(bigomega(n)==2 && omega(n)==2 && bigomega(n+1)==2 && omega(n+1)==2, cnt++; print1(n", ")));print;print("# = ",cnt) \(14,21,33,34,38,57,85,86,93,94\) De som van deze tien (\(n\))'s en (\(n+1\))'s zijn palindromen \(\to 555,565\). We merken op dat er zelfs drie triplets van achtereenvolgende semipriemgetallen zijn. \((33,34,35),(85,86,87)~\) en \(~(93,94,95)\) | 10.51 |