\(8\mathbf{\color{blue}{\;=\;}}2^3\to\) Machten van \(2\) kunnen nooit geschreven worden als som van opeenvolgende gehele getallen \(8\mathbf{\color{blue}{\;=\;}}3+5\mathbf{\color{blue}{\;=\;}}2^3\) (som van opeenvolgende onpare getallen) (som van opeenvolgende priemgetallen) \(8\mathbf{\color{blue}{\;=\;}}3+5\) (som van twee opeenvolgende Fibonaccigetallen en daardoor zelf een getal van dat type) \(\qquad\)(tevens het enige Fibonaccigetal dat een derdemacht is (het triviale geval \(1\) uitgesloten) \(8\mathbf{\color{blue}{\;=\;}}(0;0;2;2)\lower2pt{\Large{\color{teal}{➋}}}\to\{\#1\}\) \(8\mathbf{\color{blue}{\;=\;}}3^2-1\) \(8\mathbf{\color{blue}{\;=\;}}1^3+2^2+3^1\) \(8\mathbf{\color{blue}{\;=\;}}2!+3!\) (som van opeenvolgende faculteiten) \(8\mathbf{\color{blue}{\;=\;}}2*4=4!!\) (dubbelfaculteit → \(n!!=n*(n-2)*(n-4)*\dots\) stoppen voor eindterm \(0\) of \(1\) → \(4!!=8; 5!!=15\)) \(8\mathbf{\color{blue}{\;=\;}}1*2+2*3\) : dus \(8\) is de som van twee pronic getallen \(8\mathbf{\color{blue}{\;=\;}}(2*3*4)/3~~\) (OEIS A007290) \(8\mathbf{\color{blue}{\;=\;}}2*2^2\) (het volgende getal met dezelfde “structuur” is \(81=3*3^3\,)\) \(8\mathbf{\color{blue}{\;=\;}}\sqrt{64}\mathbf{\color{blue}{\;=\;}}6+\sqrt4\) \(8\mathbf{\color{blue}{\;=\;}}\lfloor~2^{\Large\pi}~\rfloor\) (OEIS A061294) \(8\mathbf{\color{blue}{\;=\;}}2^3~~\) (de eerste “echte” derdemacht)\(\mathbf{\color{blue}{\;=\;}}\) \(\qquad1^3+1^3+1^3+1^3+1^3+1^3+1^3+1^3\) (tweede schrijfwijze als som van derdemachten) \(\mathbf{\color{blue}{\;=\;}}\) \(\qquad\)Kortom in beknopte WARING notatie \(\mathbf{\color{blue}{\;=\;}}((0;0;0;0;0;0;0;0;2)\,(0;1;1;1;1;1;1;1;1))\lower2pt{\Large{\color{teal}{➌}}}\to\{\#2\}\) \(8\mathbf{\color{blue}{\;=\;}}\Large\frac{\sqrt{8^2\,+\,8^3}}{\lceil\sqrt{8}\,\rceil}~~\)(OEIS A087279) \(8\mathbf{\color{blue}{\;=\;}}1+2-3+4+5+6-7\) \(8\mathbf{\color{blue}{\;=\;}}\bbox[peachpuff,3px]{2^2+2^2}\mathbf{\color{blue}{\;=\;}}[2^4][4^2]-2^3\mathbf{\color{blue}{\;=\;}}312^2-46^3\) | 8.1 | ||||||||||||
\(8\mathbf{\color{blue}{\;=\;}}\)(som van drie derdemachten) \(\qquad\)Er zijn heel veel mogelijke oplossingen ! Cfr. machten \(2^4,3^3,\ldots\) \(\qquad\)References Sum of Three Cubes \(\qquad\)Vertegenwoordigt n het product van een kubusgetal \(k^3\) en een getal \(m\), dan erft dit getal \(n\) alle oplossingen \(\qquad\)van het getal \(m\) op de volgende manier: \(\qquad m=x^3+y^3+z^3~~\to~~ n=k^3m=k^3(x^3+y^3+z^3)~~\to~~n=k^3m=(kx)^3+(ky)^3+(kz)^3\) \(8\mathbf{\color{blue}{\;=\;}}\)(som van vijf vijfdemachten) \(\qquad\)(fully searched up to \(z=1000)\) \(\qquad\bbox[3px,border:1px blue solid]{18^5+(-38)^5+65^5+71^5+(-78)^5}\mathbf{\color{blue}{\;=\;}}\) \(8\mathbf{\color{blue}{\;=\;}}\)(som van zeven zevendemachten) \(\qquad\bbox[3px,border:1px blue solid]{(-1)^7+2^7+(-4)^7+6^7+6^7+6^7+(-7)^7}~~\to~~\) Noteer dat \(-1+2-4+6+6+6-7=8\) | 8.2 | ||||||||||||
\(8^2\mathbf{\color{blue}{\;=\;}}\to\) als som of verschil van twee machten zie bij paginagetal \(64\) \(8^3\mathbf{\color{blue}{\;=\;}}\to\) als som of verschil van twee machten zie bij paginagetal \(512\) | 8.3 | ||||||||||||
Eén getal is gelijk aan \(8\) maal de som van de cijfers : \(72=8*(7+2)\) (OEIS A005349 - Harshad getallen) Zie ook bij en | 8.4 | ||||||||||||
| \(8\) schrijven met behulp van de cijfers \(1,2,3\) en \(4\) : \(~~2+3+4-1~~=~~4^2/(3-1)~~=~~\sqrt4*(3-1)^2~~=~~\) Vindt jij er meer ? | 8.5 | ||||||||||||
\(8^3=\underline{512}~~\) en \(~~5^3=\underline{125}~~\) bevatten dezelfde cijfers. | 8.6 | ||||||||||||
\(8\) als som van twee priemgetallen (bovendien zijn beide getallen oneven) : $$ 2\;odd\;primes \left[ \begin{matrix} \\ &3&+&5\\ \\ \end{matrix} \right. $$ \(8\) als som van drie en vier priemgetallen :$$ 3\;\&\;4\;primes \left[ \begin{matrix} &2&+&3&+&3\\ \\ &2&+&2&+&2&+&2\\ \end{matrix} \right. $$ | 8.7 | ||||||||||||
| \(8\) kan niet geschreven worden als som van verschillende driehoeksgetallen. Zie voor meer toelichting bij | 8.8 | ||||||||||||
| Voor de bewering van CATALAN, zie bij | 8.9 | ||||||||||||
| \(8*(A+B)=A*B\) heeft vier oplossingen in gehele getallen : \(8*(9+72)=9*72~~\);\(~~8*(10+40)=10*40~~\);\(~~8*(12+24)=12*24~~\)en\(~~8*(16+16)=16*16\) | 8.10 | ||||||||||||
| “Acht” is samen met “een” het enige getal in het Nederlands waarvan de letters in alfabetische volgorde staan (zie ook bij ). In het Engels is er “Forty” met dezelfde eigenschap. Het Frans is goed bedeeld met “Deux”, “Cinq”, en zelfs uitdrukkingen als “Deux * cinq = dix” en “dix * dix = cent”. | 8.11 | ||||||||||||
| \(8\) schrijven met behulp van vier identieke cijfers : \((7+7/7)!/7!\) | 8.12 | ||||||||||||
| Van de \(25\) priemgetallen tussen \(1\) en \(100\) zijn er \(8\) paren van priemtweelingen : \((3,5);(5,7);(11,13);(17,19);(29,31);(41,43);(59,61);(71,73)\) | 8.13 | ||||||||||||
| Er zijn \(4\) priemgetallen die kleiner dan \(8\) zijn : \(2,3,5\) en \(7\). Van alle getallen die kleiner dan \(8\) zijn, zijn er eveneens \(4\) die met \(8\) relatief priem zijn (hun grootste gemene deler is \(1\)), namelijk \(1,3,5\) en \(7\). Zoals het getal \(8\) zijn er nog \(6\) andere getallen met deze eigenschap : \(2,3,4,14,20\) en \(90\). Zie ook bij deze getallen | 8.14 | ||||||||||||
| \(8\) als resultaat met breuken waarin de cijfers van \(1\) tot \(9\) exact één keer voorkomen : (liefst \(46\) oplossingen) : \(25496/3187=36712/4589=36728/4591=37512/4689=37528/4691=38152/4769=41896/5237=\) \(42968/5371=46312/5789=46328/5791=46712/5839=47136/5892=47328/5916=47368/5921=\) \(51832/6479=53928/6741=54312/6789=54328/6791=54712/6839=56984/7123=58496/7312=\) \(58912/7364=59328/7416=59368/7421=63152/7894=63528/7941=65392/8174=65432/8179=\) \(67152/8394=67352/8419=67512/8439=71456/8932=71536/8942=71624/8953=71632/8954=\) \(73248/9156=73264/9158=73456/9182=74528/9316=74568/9321=74816/9352=75328/9416=\) \(75368/9421=76184/9523=76248/9531=76328/9541=8\) \(8\) als resultaat met breuken waarin de cijfers van \(0\) tot \(9\) exact één keer voorkomen : (\(16\) oplossingen) : \(83672/10459=83752/10469=84296/10537=84632/10579=84736/10592=85392/10674=\) \(85432/10679=85936/10742=86352/10794=87456/10932=87536/10942=87624/10953=\) \(87632/10954=96584/12073=98456/12307=98760/12345=8\) | 8.15 | ||||||||||||
\(8={\Large\frac{1\;*\;2\;*\;3\;*\;4\;*\;5}{1~+~2~+~3~+~4~+~5}}~~\) (OEIS A032770) (OEIS A108552) \(8={\Large\frac{4\;*\;5\;*\;6}{4~+~5~+~6}}~~\) (OEIS A001082) (OEIS A032766) \(8=1+1+2+4=1*1*2*4\) maar ook \(8=1+1+2+2+2=1*1*2*2*2\) | 8.16 | ||||||||||||
| Pannumerieke voorstelling van \(8\) gebruik makend van de vier basisoperatoren \(+,-,*,/~~\): \(8=1+7=4*2=(9-5)*(6/3)\) Een toemaatje : met \(0\) erbij kan men het volgende resultaat bekomen : \(8=(9+7)/2=5+3=6+1+4^0\) waarbij \(4^0=1\) is. Een andere pandigitale vorm is : \(8=9-1=7+6-5=3*2+\sqrt4\) En voor wie hier de \(0\) mist kan men die ongemerkt als exponent toevoegen door \(9-1\) te vervangen door \(9-1^0\) Een derde mogelijkheid is : \(8=5+3=7+1=9-4+6/2\) | 8.17 | ||||||||||||
De volgende getallen behouden dezelfde cijfers na vermenigvuldiging met \(8\) : | 8.18 | ||||||||||||
Links en rechts van het \(=\) teken staan dezelfde cijfers : | 8.19 | ||||||||||||
| \(8^8=16777216\) en het omgekeerde getal \(61277761\) is een priemgetal.
Pari/GP code : isprime(fromdigits(Vecrev(digits(8^8))))\(\to1\) | 8.20 | ||||||||||||
| Het getal \(12345679\) (dus ZONDER de \(8\) of 'octamanco') wordt het getal van Lewis CARROLL genoemd. | 8.21 | ||||||||||||
| Een pare macht van \(8\), verminderd met \(1\), is een veelvoud van \(63\) : bvb. \(8^6-1=262143=63*4161\) Een onpare macht van \(8\), verminderd met \(1\), is een veelvoud van \(7\) : bvb. \(8^5-1=32767=7*4681\) | 8.22 | ||||||||||||
| Als som met de vier operatoren \(+-*\;/\) \(8=(2+1)+(2-1)+(2*1)+(2/1)\) | 8.23 | ||||||||||||
| Er zijn twee rechthoekige driehoeken met gehele zijden en \(8\) als één van de zijden : \((6;8;10),(8;15;17)\) | 8.24 | ||||||||||||
| Enkele merkwaardige getallenpiramides
\begin{align} 123456789*8+9&=987654321\\ 12345678*8+8&=98765432\\ 1234567*8+7&=9876543\\ 123456*8+6&=987654\\ 12345*8+5&=98765\\ 1234*8+4&=9876\\ 123*8+3&=987\\ 12*8+2&=98\\ 1*8+1&=9 \end{align} \begin{align} 8*4&=32&8*9&=72\\ 98*34&=3332&98*79&=7742\\ 998*334&=333332&998*779&=777442\\ 9998*3334&=33333332&9998*7779&=77774442\\ 99998*33334&=3333333332&99998*77779&=7777744442\\ 999998*333334&=333333333332&999998*777779&=777777444442\\ 9999998*3333334&=33333333333332&9999998*7777779&=77777774444442\\ 99999998*33333334&=3333333333333332&99999998*77777779&=7777777744444442\\ \cdots&=\cdots&\cdots&=\cdots \end{align} \begin{align} 88&=9*9+7\\ 888&=9*98+6\\ 8888&=9*987+5\\ 88888&=9*9876+4\\ 888888&=9*98765+3\\ 8888888&=9*987654+2\\ 88888888&=9*9876543+1\\ 88888888&=9*98765432+0\\ 888888888&=9*987654321-1\\ \cdots&=\cdots \end{align} \begin{align} 8*12+2&=98\\ 8*123+3&=987\\ 8*1234+4&=9876\\ 8*12345+5&=98765\\ \cdots&=\cdots \end{align} \begin{align} 11111111*88888888&=987654301234568\\ 1111111*8888888&=9876541234568\\ 111111*888888&=98765234568\\ 11111*88888&=987634568\\ 1111*8888&=9874568\\ 111*888&=98568\\ 11*88&=968\\ 1*8&=8 \end{align} \begin{align} 8*8+13&=77\\ 88*8+13&=717\\ 888*8+13&=7117\\ 8888*8+13&=71117\\ 88888*8+13&=711117\\ 888888*8+13&=7111117\\ 8888888*8+13&=71111117\\ \cdots&=\cdots \end{align} | 8.25 | ||||||||||||
| Volgens het theorema van WARING kunnen alle gehele getallen voorgesteld worden als de som van ten hoogste negen derdemachten. De meeste getallen kunnen voorgesteld worden als de som van \(8\) derdemachten. Er zijn slechts twee uitzonderingen : voor \(23\) en \(239\) zijn negen derdemachten nodig. Zie ook (OEIS A002804) | 8.26 | ||||||||||||
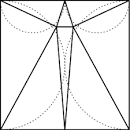
Om een vierkant in scherphoekige driehoeken te verdelen zijn minimaal \(8\) driehoeken nodig.
(Web-bron van de afbeelding) Zie ook voor het geval met gelijkbenige driehoeken. | 8.27 | ||||||||||||
| Een horizontaal geplaatste \(8\) is het teken voor oneindig : \(\large{\infty}\) | 8.28 | ||||||||||||
| EEN PUZZEL
\(\bbox[3px,border:1px solid blue]{\;Opgave\;}\) | 8.29 | ||||||||||||
| EEN PUZZEL
\(\bbox[3px,border:1px solid blue]{\;Opgave\;}\) | 8.30 | ||||||||||||
| WETENSWAARD
\(8^3=512\) en de som van de cijfers \(5+1+2=8\) is terug het grondtal. Naast \(8\) zijn nog vijf andere getallen met | 8.31 | ||||||||||||
| \(8\approx\Large{987654321\over123456789}\) omdat de deling gelijk is aan \(8.0000000729000006633900060368490549353\ldots\) Maar verwissel de twee laatste cijfers van de teller en we bekomen wel degelijk \(8=\Large{9876543\color{blue}{12}\over123456789}\) | 8.32 | ||||||||||||
| Men moet \(8\) tot minimaal de \(55\)ste macht verheffen opdat in de decimale expansie exact acht achten verschijnen. \(8^{55}=4676{\color{blue}{8}}0523945{\color{blue}{888}}933{\color{blue}{8}}251791464692105662{\color{blue}{8}}9{\color{blue}{8}}9{\color{blue}{8}}41375232\qquad\) (OEIS A244603) | 8.33 | ||||||||||||
Er zijn \(3\) getallen van acht cijfers die gelijk zijn aan de som van de \(achtste\) macht van hun cijfers : \(24678050=2\)\(^8\)\(\,+\,4\)\(^8\)\(\,+\,6\)\(^8\)\(\,+\,7\)\(^8\)\(\,+\,8\)\(^8\)\(\,+\,0\)\(^8\)\(\,+\,5\)\(^8\)\(\,+\,0\)\(^8\) De overige twee getallen zijn : \(24678051,88593477\) | 8.34 | ||||||||||||
Alle getallen van \(1\) tot \(8\) worden gebruikt, hetzij als grondtal hetzij als exponent, in deze gelijkheden van producten van machten. Verdeelsleutels \([1-3]\) en \([2-2]\) leveren elk \(2\) zuivere oplossingen maar door het feit dat \({\color{tomato}{1}}^n\) als invariante kan switchen van links naar rechts zijn het eigenlijk dezelfde oplossingen. \begin{align} 4^7&\mathbf{\color{blue}{\;=\;}}{\color{tomato}{1^6}}*2^5*8^3\\ 8^5&\mathbf{\color{blue}{\;=\;}}{\color{tomato}{1^7}}*2^3*4^6\\ \\ {\color{tomato}{1^6}}*4^7&\mathbf{\color{blue}{\;=\;}}2^5*8^3\\ {\color{tomato}{1^7}}*8^5&\mathbf{\color{blue}{\;=\;}}2^3*4^6\\ \end{align} | 8.35 | ||||||||||||
\(8*10\)\(^{8}\)\(\,-\,1~~\) is een veralgemeend Woodall priemgetal, de derde in zijn soort (\(k*10^k-1\)). | 8.36 | ||||||||||||
\(8\) en \(9\) zijn het enige paar van opeenvolgende gehele getallen die ook niet triviale machten van gehele getallen zijn, | 8.37 | ||||||||||||
John Baez uit California geeft een lezing aan de universiteit van Glasgow over het getal \(8\), één van zijn favorieten. | 8.38 | ||||||||||||
\(8!!-1~~\)is een priemgetal van \(3\) cijfers lang (\(383\)). (OEIS A007749) (Dubbelfaculteit) Pari/GP code : isprime(prod(i=1,8/2,2*i)-1) → 1 (true) | 8.39 | ||||||||||||
\(8\) is de som van de 'som der delers' van de getallen van \(1\) tot \(3\) : \((1)+(1+2)+(1+3)\) | 8.40 | ||||||||||||
Som der reciproken van partitiegetallen van \(8\) levert nooit \(1\) op. Bijgevolg ook geen partities met unieke termen. | 8.41 | ||||||||||||
\(8\)\(^{1}\)\(+8\)\(^{0}\)\(+8\)\(^{3}\)\(+8\)\(^{3}\)\(\mathbf{\color{blue}{\;=\;}}1033\to\) en tevens een priemgetal\(~~\) (OEIS A236067) | 8.42 | ||||||||||||
\(8=2^3={\Large\frac{6!}{3!\,*\,5!!}}\) | 8.43 | ||||||||||||
○–○–○ \(8^2=64~~\) en \(~~6+\sqrt4=8\)\(\bbox[2px,border:1px solid green]{8^3=512~~~\text{en}~~~5+1+2=8}\) Zie ook bij (RightClick + Esc) \(8^4=4096~~\) en \(~~4+0!+9-6=8\) \(8^5=32768~~\) en \(~~3-2-7+6+8=8\) \(8^6=262144~~\) en \(~~2-6+2+14-4=8\) \(8^7=2097152~~\) en \(~~2+0-9+7+1+5+2=8\) \(8^8=16777216~~\) en \(~~16+7+7-7-21+6=8\) \(8^9=134217728~~\) en \(~~134-21-77-28=8\) \(8^{10}=1073741824~~\) en \(~~107-3-7-4+1-82-4=8\) \(8^{11}=8589934592~~\) en \(~~85-89+9-3+4-5+9-2=8\) \(8^{12}=68719476736~~\) en \(~~68+7+1-9+4+7-67+3-6=8\) \(8^{13}=549755813888~~\) en \(~~549+7-558-1+3+8+8-8=8\) \(8^{14}=4398046511104~~\) en \(~~43+9+8+0+46-5+11-104=8\) \(8^{15}=35184372088832~~\) en \(~~3+5-18+4+3+7-20+8-8-8+32=8\) \(8^{16}=281474976710656~~\) en \(~~28-1+4-7-4-9-7+67-1+0-6-56=8\) \(8^{17}=2251799813685248~~\) en \(~~22-51+7+9+9+8+13+6-8-5+2+4-8=8\) \(8^{18}=18014398509481984~~\) en \(~~18+0+1+4+3-9-8-5+0+9-4-8+19-8-4=8\) \(8^{19}=144115188075855872~~\) en \(~~14+4-1-1+5-1-8-8+0+75+8+5+5-87-2=8\) \(8^{20}=1152921504606846976~~\) en \(~~11+5-29-2+15+0+4+60+6-8-46-9+7-6=8\) | 8.44 | ||||||||||||
Som Der Cijfers (\(sdc\)) van \(k^{\large{8}}\) is gelijk aan het grondtal \(k\). De triviale oplossingen \(0\) en \(1\) negerend vinden we : \(\qquad\qquad~sdc\left(46^{\large{8}}\right)=46\qquad\qquad~sdc\left(54^{\large{8}}\right)=54\qquad\qquad~sdc\left(63^{\large{8}}\right)=63\) | 8.45 | ||||||||||||
| Exponent \(8\) heeft geen groter grondtal dan \(712\) zodat de decimale expansie van deze macht geen cijfers bevat uit het grondtal\(~~~~\to~~~~712^{8}=66045000696445844586496\) (OEIS A113951) | 8.46 | ||||||||||||
| Expressie van \(n\) enkel gebruik makend van faculteiten, vierkantswortels en afrondingen. \(8~=~\)prod(i=1,ceil(sqrt(ceil(sqrt(ceil(sqrt(8!))))))/2,2*i) in Pari/GP code \(\qquad\qquad8=\)\({\huge\lceil}\)\(\!\sqrt{{\huge\lceil}\sqrt{\lceil\sqrt{8!}\,\rceil}{\huge\,\rceil}}\)\({\,\huge\rceil}!!\) | 8.47 | ||||||||||||
Als expressie met enkelcijferige toepassing, resp. van \(1\) tot \(9~~\) (met dank aan Inder. J. Taneja). | 8.48 | ||||||||||||
Met de cijfers van \(1\) tot \(9\) in stijgende en dalende volgorde (met dank aan Inder. J. Taneja) : | 8.49 | ||||||||||||
| Het kleinste getal dat exact \(8\) delers heeft is \(24=2^3*3\). (OEIS A005179) | 8.50 | ||||||||||||
| \(k=8\) is een potentievol getal (Eng. powerful number) maar ook de priemfactor van \(k+1=9\) is potentievol. \(8=2^3~~\) en \(~~9=3^2~~\) (OEIS A060355) | 8.51 | ||||||||||||
| EEN PUZZEL
\(\bbox[3px,border:1px solid blue]{\;Opgave\;}\) Heb je het opgegeven na meerdere pogingen dan is de oplossing te vinden in de broncode van deze webpagina (Ctrl+U). | 8.52 | ||||||||||||
| Zowel de helft \((4)\) als het dubbel \((16)\) van \(8\) zijn kwadraten. Zie ook (OEIS A001105) | 8.53 | ||||||||||||
| \(8\) is het aantal partities van \(9\) met verschillende termen. (OEIS A000009) Onderstaande Pari/GP code zet ze allemaal op een rijtje. q=partitions(9); c=0; for(i=1,#q, z=q[i]; f=1; for(j=1,#z-1, if(z[j]==z[j+1], f*=0));if(f, c++; print(c," ",q[i]))) | 8.54 | ||||||||||||
| De som van vier positieve \(8ste\) machten is gelijk aan de som van vier andere positieve \(8ste\) machten: \(\qquad\qquad861^8+1953^8+2012^8+3113^8=1128^8+2557^8+2767^8+2823^8\) De som is een getal van \(28\) cijfers \(\to~~9299777658352887974911487459\) Het was Nuutti Kuosa die deze oplossing \((8\text{-}4\text{-}4)\) gevonden heeft in \(2006~~\). (Minimal Equal Sums Of Like Powers) Er bestaan ook sommen van \(8\) achtstemachten die gelijk zijn aan één achtstemacht. Hier is de kleinste: \(1409^8=90^8+223^8+478^8+524^8+748^8+1088^8+1190^8+1324^8\) | 8.55 | ||||||||||||
(drie multigrades) \(8\to8^5\to\) \begin{aligned} 8^1&=21^1+43^1-62^1-68^1+74^1\\ 8^5&=21^5+43^5-62^5-68^5+74^5\\ \\ 8^1&=-82^1-142^1+234^1+502^1-504^1\\ 8^5&=-82^5-142^5+234^5+502^5-504^5\\ \\ 8^1&=-182^1-203^1+404^1+651^1-662^1\\ 8^5&=-182^5-203^5+404^5+651^5-662^5\\ \end{aligned} | 8.56 | ||||||||||||
Gegeven dat vier punten op een cirkel verbonden worden door lijnen (diagonalen) dan is het grootste aantal regio's \(8\). (OEIS A000127) (Wikipedia) (How many regions can be formed by the chords joining n points on a circle?) | 8.57 | ||||||||||||
\(8\mathbf{\color{blue}{\;=\;}}9^2+36^2-37^2\mathbf{\color{blue}{\;=\;}}9+36-37\) \(8\mathbf{\color{blue}{\;=\;}}10^2+22^2-24^2\mathbf{\color{blue}{\;=\;}}10+22-24\) \(8\mathbf{\color{blue}{\;=\;}}12^2+15^2-19^2\mathbf{\color{blue}{\;=\;}}12+15-19\) | 8.58 |