\(5\mathbf{\color{blue}{\;=\;}}2+3\) (som van opeenvolgende gehele getallen) (som van de eerste twee priemgetallen) \(5\mathbf{\color{blue}{\;=\;}}2+3\) (som van twee opeenvolgende Fibonaccigetallen en daardoor zelf een getal van dat type) \(\qquad\)Het vijfde Fibonaccigetal is gelijk aan \(5\) (alleen \(1\) is nog een Fibonaccigetal dat gelijk is aan zijn rang) \(\qquad\)en \(F(5)\) is een priemgetal, de derde in zijn soort (OEIS A005478) (OEIS A001605) \(5\mathbf{\color{blue}{\;=\;}}(0;0;1;2)\lower2pt{\Large{\color{teal}{➋}}}\to\{\#1\}\) \(5\mathbf{\color{blue}{\;=\;}}1^2+2^2\) (som van opeenvolgende kwadraten) \(5\mathbf{\color{blue}{\;=\;}}\)(som van vijf positieve derdemachten) \(1^3+1^3+1^3+1^3+1^3\mathbf{\color{blue}{\;=\;}}(0;0;0;0;1;1;1;1;1)\lower2pt{\Large{\color{teal}{➌}}}\to\{\#1\}\) \(5\mathbf{\color{blue}{\;=\;}}3!-2!+1!\) \(5\mathbf{\color{blue}{\;=\;}}2^2+1\) \(5\mathbf{\color{blue}{\;=\;}}3!-1\) \(5\mathbf{\color{blue}{\;=\;}}1*1!+2*2!\) \(5\mathbf{\color{blue}{\;=\;}}\sqrt{1*2*3*4+1}\mathbf{\color{blue}{\;=\;}}1+(1+1)^2~~\) (product van vier opeenvolgende getallen plus \(1\) is een kwadraat) \(\qquad\)(OEIS A028387) \(5\mathbf{\color{blue}{\;=\;}}2*3*4*5/24~~\) (product van vier opeenvolgende getallen is deelbaar door \(24\)) (OEIS A000332) \(5\mathbf{\color{blue}{\;=\;}}\sqrt{1+3+5+7+9}~~\) (vierkantswortel uit de som van opeenvolgende onpare getallen) \(5\mathbf{\color{blue}{\;=\;}}{\Large\frac{3\;*\;4\;*\;5}{3~+~4~+~5}}~~\) (OEIS A001082) (OEIS A032766) \(5\mathbf{\color{blue}{\;=\;}}\Large\frac{\sqrt{5^3\,-\,5^2}}{\lfloor\sqrt{5}\,\rfloor}~~\)(OEIS A087279) \(5\mathbf{\color{blue}{\;=\;}}2^5-3^3\mathbf{\color{blue}{\;=\;}}\bbox[2px,border:1px brown dashed]{3^2-2^2}\) | 5.1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\(5\mathbf{\color{blue}{\;=\;}}\)(som van drie derdemachten) \(\qquad\)References Sum of Three Cubes \(\qquad\)Getallen van de vorm \(~9m+4~\) of \(~9m+5~\) kunnen nooit als som van drie derdemachten geschreven worden. \(\qquad\)In dit geval is \(m=0~~(+5)\). \(5\mathbf{\color{blue}{\;=\;}}\)(som van vier derdemachten) \(\qquad(z\gt1000)\) \(5\mathbf{\color{blue}{\;=\;}}\)(som van vijf vijfdemachten) \(\qquad\)(fully searched up to \(z=1000)\) \(\qquad\bbox[3px,border:1px blue solid]{1^n+1^n+1^n+1^n+1^n}~~(n=5)\mathbf{\color{blue}{\;=\;}}\) | 5.2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\(5^2\mathbf{\color{blue}{\;=\;}}\to\) als som of verschil van twee machten zie bij paginagetal \(25\) \(5^3\mathbf{\color{blue}{\;=\;}}\to\) als som of verschil van twee machten zie bij paginagetal \(125\) | 5.3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Eén getal is gelijk aan \(5\) maal de som van zijn cijfers : \(45=5*(4+5)\) (OEIS A005349 - Harshad getallen) | 5.4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Alle machten van \(5\) eindigen op het cijfer \(5\). De enige uitzondering is \(5^0=1\). \(5\) is het enige priemgetal dat zowel met zijn voorganger \(3\) als met zijn opvolger \(7\) telkens een priemtweeling vormt. \(5\) is ook het enige priemgetal dat zowel de som als het verschil van twee priemgetallen is : \(2+3~~\) en \(~~7-2\) \(5\) als som van priemgetallen kan louter op deze enkele wijze : $$ 2\;primes \left[ \begin{matrix} \\ &2&+&3\\ \\ \end{matrix} \right. $$ | 5.5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Behalve het getal \(5\) zelf, is er geen enkel priemgetal dat eindigt op \(5\). | 5.6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\(5^2=1!+4!\) \(5^3=125\) en dit is niets anders dan \(1^2\;(=1)\) en \(5^2\;(=25)\) achter elkaar geschreven. | 5.7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(5^4\mathbf{\color{blue}{\;=\;}}2^4+2^4+3^4+4^4+4^4\mathbf{\color{blue}{\;=\;}}7^2+24^2\mathbf{\color{blue}{\;=\;}}625\) | 5.8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(5^0+5^1+5^2~~\mathbf{\color{blue}{\;=\;}}~~2^0+2^1+2^2+2^3+2^4~~\) (waarschijnlijk is deze vorm uniek voor priemgetallen als grondtal) | 5.9 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(5*(A+B)=A*B\) heeft twee oplossingen in gehele getallen : \(5*(6+30)=6*30~~\) en \(~~5*(10+10)=10*10\) | 5.10 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Probleem van BROCARD : \(5!+1=121=11^2\) (zie voor meer uitleg bij ) | 5.11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(8-3=5~~\) en \(~~8^2-3^2=55\) | 5.12 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(5^3=125~~\) en \(~~8^3=512~~\) bevatten dezelfde cijfers. | 5.13 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Beschouw vijf opeenvolgende getallen en brengt men elk getal tot eenzelfde macht die niet gelijk is aan de vierde macht of een veelvoud van vier, en maakt men de som van deze vijf tot een macht verheven getallen, dan is die som steeds deelbaar door \(5\). Bvb. We nemen de opeenvolgende getallen \(3;4;5;6\) en \(7\) en we zetten alles tot de derde macht. De som is dan \(3^3+4^3+5^3+6^3+7^3=27+64+125+216+343=775=5*155\) Met bvb. een vierde macht lukt dit niet : \(2^4+3^4+4^4+6^4+6^4=2274\) (geen vijfvoud). Deze eigenschap geldt ook voor de eerste macht. Dus de som van vijf opeenvolgende getallen is een vijfvoud. En dit geldt ook voor vijf opeenvolgende getallen uit een rekenkundige rij. Zo is er bvb. de rij \(8;11;14;17;20\) waarvan de som \(70=5*14\) is. | 5.14 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(5\) kan niet geschreven worden als som van verschillende driehoeksgetallen. Zie voor meer toelichting bij | 5.15 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Er zijn \(5\) regelmatige (Platonische) veelvlakken in de ruimte : tetraëder, kubus, octaëder, dodecaëder, icosaëder (respectievelijk : regelmatig \(4-, 6-, 8-, 12-\) en \(20-vlak\)). | 5.16 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| De kleinste rechthoekige driehoek met gehele getallen als zijden heeft als afmetingen \(3*4*5\), waarbij de stelling van Pythagoras geldt : \(3^2+4^2=5^2\). Er bestaat ook een rechthoekige driehoek met rechthoekszijde \(5\) en met gehele afmetingen voor de zijden : de driehoek \(5*12*13\) waarvoor geldt dat \(5^2+12^2=13^2\). Er zijn dus twee rechthoekige driehoeken met gehele zijden en waarvan één zijde \(5\) is : \((3;4;5)\) en \((5;12;13)\) | 5.17 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Er zijn \(5\) driehoeken met gehele zijden en waarbij de getalwaarden van omtrek en oppervlakte dezelfde zijn. De zijden van die vijf driehoeken zijn : \((5;12;13),(6;8;10),(6;25;29),(7;15;20)\) en \((9;10;17)\). Hiervan zijn de eerste twee driehoeken rechthoekig. Wie dit wil controleren kan de formule van HERON gebruiken : Formule van HERON Berekening van de oppervlakte van een driehoek als de lengten van de drie zijden \((a,b,c)\) gekend zijn. We berekenen eerst \(s={\large\frac{(a+b+c)}{2}}~~\) (\(s\) is dus de halve omtrek van de driehoek). Dan berekenen we het product \(A^2=s*(s-a)*(s-b)*(s-c)\). De oppervlakte is dan de vierkantswortel uit \(A^2\). (Formule van Heron) | 5.18 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Voor vergelijkingen van de eerste, tweede, derde of vierde graad bestaan formules om deze op te lossen (voor de derde graad en zeker voor de vierde graad zijn dit behoorlijk complexe formules). Vanaf de \(vijfde\) graad is het onmogelijk (en ook bewezen) een algemene oplossing te vinden voor dergelijke vergelijkingen. Baanbrekend werk hieromtrent werd geleverd door twee jong gestorven wiskundigen : Niels Henrik ABEL en Evariste GALOIS. | 5.19 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(5\) als resultaat met breuken waarin de cijfers van \(1\) tot \(9\) exact één keer voorkomen : (12 oplossingen) \(13485/2697=13845/2769=14685/2937=14835/2967=14865/2973=16485/3297=\) \(18645/3729=31485/6297=38145/7629=46185/9237=48135/9627=48615/9723=5\) \(5\) als resultaat met breuken waarin de cijfers van \(0\) tot \(9\) exact één keer voorkomen : (12 oplossingen) \(67290/13458=67920/13584=69270/13854=72690/14538=72930/14586=73290/14658=\) \(76920/15384=79230/15846=79320/15864=92670/18534=92730/18546=93270/18654=5\) | 5.20 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
De volgende getallen behouden dezelfde cijfers na vermenigvuldiging met \(5\) : | 5.21 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Even machten van \(5\), verminderd met \(1\), zijn deelbaar door \(24\) : | 5.22 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
De volgende getallenpiramide heeft uitkomsten die alle op \(5\) eindigen : \begin{align} 3^2-2^2&=\mathbf5\\ 3^4-2^4&=6\mathbf5\\ 3^6-2^6&=66\mathbf5\\ 3^8-2^8&=630\mathbf5\\ 3^{10}-2^{10}&=5802\mathbf5\\ \cdots&=\cdots \end{align} | 5.23 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Deze getallenpiramide heeft \(49\) als centrale substring in het product : \begin{align} 5*99&=\mathbf{49}5\\ 55*999&=5\mathbf{49}45\\ 555*9999&=55\mathbf{49}445\\ 5555*99999&=555\mathbf{49}4445\\ 55555*999999&=5555\mathbf{49}44445\\ 555555*9999999&=55555\mathbf{49}444445\\ 5555555*99999999&=555555\mathbf{49}4444445\\ \cdots&=\cdots \end{align} | 5.24 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Een figuur met een combinatie van \(vijf\) vierkantjes is een pentomino. Er zijn twaalf mogelijke combinaties van \(vijf\) vierkantjes mogelijk (spiegelingen niet meegerekend). Er zijn tal van mogelijke puzzels waarbij bvb. een rechthoek van bepaalde afmetingen moet worden opgevuld met pentominoes. Zie ook bij en In de volgorde van de figuur luidt de bovenste rij : F(R); V; L(Q); N(S); P; T en de onderste rij U; I(O); W; X; Y; Z. De benamingen zijn uitgedacht door GOLOMB; tussen haakjes staat de alternatieve benaming afkomstig van CONWAY. De benamingen volgens GOLOMB zijn algemeen gebruikelijk; de benamingen volgens CONWAY zijn de opeenvolgende letters van O tot en met Z. (Wikipedia) | 5.25 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Op een schaakbord zijn minimaal \(5\) koninginnen nodig om alle vakjes te kunnen aanvallen : Een mogelijke schikking is de volgende :
| 5.26 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| EEN WEETJE
Het kwadraat van een getal eindigend op \(5\) kan gemakkelijk berekend worden op de volgende manier : | 5.27 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| WETENSWAARD
Er zijn slechts drie priemgetallen van de vorm \(n^n+1\) (OEIS A121270) : | 5.28 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| EEN PROBLEEM
\(\bbox[3px,border:1px solid blue]{\;Opgave\;}\) | 5.29 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(5\) schrijven met behulp van de cijfers \(1,2,3\) en \(4\) : \(~~12-3-4~~=~~(4+1)*(3-2)~~=~~\sqrt{(4+1)*(2+3)}~~=~~\) Vindt jij er meer ? | 5.30 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Men moet \(5\) tot minimaal de \(30\)ste macht verheffen opdat in de decimale expansie exact vijf vijven verschijnen. \(5^{30}= 931322{\color{blue}{5}}7461{\color{blue}{5}}478{\color{blue}{5}}1{\color{blue}{5}}62{\color{blue}{5}}\qquad\) (OEIS A244603) | 5.31 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(5\) is één van drie gekende WILSON priemgetallen zodanig dat \((p-1)!~~\)≡\(~-1~(mod~p^2)\). Dit betekent dat na de modulus operatie \(p=5;~Mod((p-1)!,p^2)\) het absolute verschil tussen de termen gelijk is aan \(1\). Doe bvb. met pari/gp het commando \(p=5;~(p-1)!~\&~(p^2)\). Het antwoord luidt \(1\). Zo ook voor \(p=13\) en \(p=563\). Zie bij en en (OEIS A007540) | 5.32 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Het volgende patroon is uniek. Men kan in de gelijkheid \(+\) en \(*\) verwisselen : | 5.33 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
De eerste keer dat er \(5\) opeenvolgende samengestelde getallen voorkomen gebeurt tussen de priemgetallen \(23\) en \(29\) | 5.34 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Er zijn \(2\) getallen van vier cijfers die gelijk zijn aan de som van de vijfde macht van hun cijfers : \(4150=4\)\(^5\)\(\,+\,1\)\(^5\)\(\,+\,5\)\(^5\)\(\,+\,0\)\(^5\) \(4151=4\)\(^5\)\(\,+\,1\)\(^5\)\(\,+\,5\)\(^5\)\(\,+\,1\)\(^5\) Er zijn \(3\) getallen van vijf cijfers die gelijk zijn aan de som van de vijfde macht van hun cijfers : \(54748=5\)\(^5\)\(\,+\,4\)\(^5\)\(\,+\,7\)\(^5\)\(\,+\,4\)\(^5\)\(\,+\,8\)\(^5\) De overige twee getallen zijn : \(92727,93084\) Er is \(1\) getal van zes cijfers die gelijk is aan de som van de vijfde macht van hun cijfers : \(194979=1\)\(^5\)\(\,+\,9\)\(^5\)\(\,+\,4\)\(^5\)\(\,+\,9\)\(^5\)\(\,+\,7\)\(^5\)\(\,+\,9\)\(^5\) | 5.35 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\(2\)\(^{5}\)\(\,+\,5~~\) is een priemgetal, de derde in zijn soort. (OEIS A052007) | 5.36 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
John Baez uit California geeft een lezing aan de universiteit van Glasgow over het getal \(5\), één van zijn favorieten. | 5.37 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\(F(5)~=~5~~\)is een Fibonacci priemgetal. (OEIS A001605) (OEIS A005478) | 5.38 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
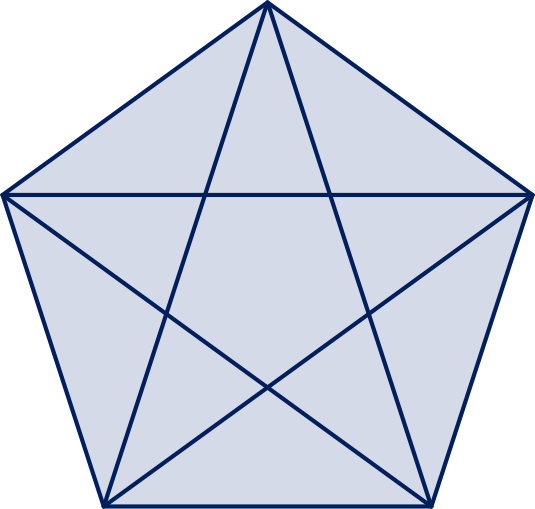
Er zijn \(5\) diagonalen binnen in een reguliere vijfhoek \(n=5\). Het aantal diagonalen van een veelhoek met \(n\) hoeken is als volgt te berekenen \({\Large\frac{n(n-3)}{2}}\) voor \(n\gt3\)
\(5\) is ook het aantal snijpunten gemaakt door de vijf diagonalen 'binnen' in een reguliere vijfhoek. \(5\) is ook het aantal snijpunten gemaakt door de diagonalen en hoekpunten in een reguliere vierhoek of vierkant. | 5.39 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
De volgende formule levert getallen die deelbaar zijn door \(5\) \(\bbox[3px,border:1px solid]{4^n-3^n+2^n-1^n}\) maar enkel op voorwaarde dat het even machten zijn. | 5.40 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Primoriaal van \(5\) min \(1\) (\(5\#-1\)) is een priemgetal. \(2*3*{\color{blue}{5}}-1=29\) | 5.41 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \((5^{5}-5!)/5\) is een priemgetal \((=601)\), de tweede in zijn soort \((p^p-p!)/p)~~\) (OEIS A137999) | 5.42 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\(2\)\(^{5}\)\(\,-\,3\) is een priemgetal \((=29)\), de derde in zijn soort \((2^k-3)~~\) (OEIS A050414) | 5.43 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\(5\) als expressie met de cijfers van \(1\) tot \(9\) \(5=-21+3-4+5-76+98={\Large{{7\over{6\,*\,4}}+{5\over{8\,*\,3}}+{9\over{2\,*\,1}}}}\) | 5.44 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Som der reciproken van partitiegetallen van \(5\) levert nooit \(1\) op. Bijgevolg ook geen partities met unieke termen. | 5.45 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\((5\)\(^{5}\)\(+1)/(5+1)\) is een priemgetal \((=521)\), de tweede in zijn soort \((p^p+1)/(p+1)~~\) (OEIS A056826) | 5.46 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\(5!+2\)\(^{5}\)\(\,-\,1\) is een priemgetal \((=151)\), de vierde in zijn soort \((k!+2^k-1)~~\) (OEIS A186449) | 5.47 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\(5\)\(^{3}\)\(+5\)\(^{9}\)\(+5\)\(^{0}\)\(+5\)\(^{9}\)\(+5\)\(^{5}\)\(+5\)\(^{1}\)\(+5\)\(^{1}\)\(\mathbf{\color{blue}{\;=\;}}3909511~~\) (OEIS A236067) | 5.48 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\(5\) heeft een priem aantal partities, namelijk \((7)~~\) (OEIS A046063) (OEIS A049575) | 5.49 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
○–○–○ \(5^2=25~~\) en \(~~ !(!2)+5=5\)\(5^3=125~~\) en \(~~(-1+2)*5=5\) \(5^4=625~~\) en \(~~(6-prime(prime(2)))*5=5\) \(5^5=3125~~\) en \(~~3-1-2+5=5\) \(5^6=15625~~\) en \(~~1+5+6-2-5=5\) \(5^7=78125~~\) en \(~~7-8-1+2+5=5\) \(5^8=390625~~\) en \(~~3+9+0*6-2-5=5\) \(5^9=1953125~~\) en \(~~19-5-3+1-2-5=5\) \(5^{10}=9765625~~\) en \(~~9-76+5+62+5=5\) \(5^{11}=48828125~~\) en \(~~48-8-28-12+5=5\) \(5^{12}=244140625~~\) en \(~~24+4-14+0-6+2-5=5\) \(5^{13}=1220703125~~\) en \(~~12+20+7+0-31+2-5=5\) \(5^{14}=6103515625~~\) en \(~~610+35-15-625=5\) \(5^{15}=30517578125~~\) en \(~~30+51-75-7+8+1+2-5=5\) \(5^{16}=152587890625~~\) en \(~~152+5-8-78-9+0-62+5=5\) \(5^{17}=762939453125~~\) en \(~~762-939+4+53+125=5\) \(5^{18}=3814697265625~~\) en \(~~381-469+7+2+65-6+25=5\) \(5^{19}=19073486328125~~\) en \(~~19+0-7+3-4-8+6+3+2+8-12-5=5\) \(5^{20}=95367431640625~~\) en \(~~9+5+3-6-7-4+3+1+6+4+0-6+2-5=5\) | 5.50 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Som Der Cijfers (\(sdc\)) van \(k^{\large{5}}\) is gelijk aan het grondtal \(k\). De triviale oplossingen \(0\) en \(1\) negerend vinden we : \(\qquad\qquad~sdc\left(28^{\large{5}}\right)=28\qquad\qquad~sdc\left(35^{\large{5}}\right)=35\qquad\qquad~sdc\left(36^{\large{5}}\right)=36\) \(\qquad\qquad~sdc\left(46^{\large{5}}\right)=46\) | 5.51 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Expressie van \(n\) enkel gebruik makend van faculteiten, vierkantswortels en afrondingen. \(5~=~\)ceil(sqrt(ceil(sqrt(ceil(sqrt(5!))))!)) in Pari/GP code \(\qquad\qquad5={\Huge\lceil}{\sqrt{{\huge\lceil}{\sqrt{{\large\lceil}{\sqrt{5!}}~{\large\rceil}~}}~{\huge\rceil}!}}~~{\Huge\rceil}\) | 5.52 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Het kwadraat van \(5\) kan uitgedrukt worden als een som van verschillende faculteiten. \(5^2=25=1!+4!~~\) (OEIS A014597) In totaal zijn er maar \(15\) getallen van deze soort gekend. | 5.53 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(5\) is het aantal partities van \(4~~\) (OEIS A000041) Pari/GP code : numbpart(4) | 5.54 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Als expressie met enkelcijferige toepassing, resp. van \(1\) tot \(9~~\) (met o.a. dank aan Inder. J. Taneja). | 5.55 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Met de cijfers van \(1\) tot \(9\) in stijgende en dalende volgorde (met dank aan Inder. J. Taneja) : | 5.56 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\(5={\Large\frac{4!-4}{4}}\) | 5.57 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(5^2+2\) is een machtsrijk (Eng. powerful) getal \((=27=3^3)\), de eerste in zijn soort \((k^2+2).\) (OEIS A175180) | 5.58 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(5\) is het kleinste priemgetal \(p\) waarbij \(p-1\) èn \(p+1\) beide \(n=2\) priemfactoren hebben (met meervoudigheid). \(4=2*2~~\) en \(~~6=2*3\) Voor andere waarden van \(n\geqslant2\) zie (OEIS A154598) | 5.59 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(5\) is een getal dat behoort tot een set van vijf priemgetallen, namelijk \(~(5,11,17,23,29)~\) waarvan het verschil \(6\) is. | 5.60 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Machten van \(5\) als som van twee kwadraten met groter wordende grondtallen : \(\qquad\qquad5^1=1^2+2^2\) \(\qquad\qquad5^2=3^2+4^2\) \(\qquad\qquad5^3=5^2+10^2\) \(\qquad\qquad5^4=15^2+20^2\) \(\qquad\qquad5^5=25^2+50^2\) \(\qquad\qquad5^6=75^2+100^2\) \(\qquad\qquad5^7=125^2+250^2\) \(\qquad\qquad5^8=375^2+500^2\) \(\qquad\qquad5^9=625^2+1250^2\) | 5.61 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Schikkingen met identieke getallen met o.a. machten en/of faculteiten \(\qquad\qquad5=4!/4-4/4\) \(\qquad\qquad5=(44-4!)/4\) \(\qquad\qquad5=5!/(5*5-5^0)\) | 5.62 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Een opmerkelijke identiteit | 5.63 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| EEN PUZZEL
Het resultaat van een reeks van vijf bewerkingen is altijd \(1089\) : | 5.64 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Het omgekeerde van \(2^{5}=32\) is een priemgetal \(\to{23}\) Pari/GP code : isprime(fromdigits(Vecrev(digits(2^5))))\(\to1=\) true Als we de cijfers uit de decimale expansie van \(2\)\(^{5}\)\(=32\) rangschikken in stijgende orde dan bekomen we een priemgetal \(23\) met lengte \(2\). Pari/GP code : isprime(fromdigits(vecsort(digits(2^5))))\(\to1=\) true | 5.65 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Het omgekeerde van \(4^{5}=1024\) is een priemgetal \(\to{4201}\) Pari/GP code : isprime(fromdigits(Vecrev(digits(4^5))))\(\to1=\) true | 5.66 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Het kleinste getal dat exact \(5\) delers heeft is \(16=2^4\). (OEIS A005179) | 5.67 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(5\) is het aantal partities van \(7\) met verschillende termen. (OEIS A000009) Onderstaande Pari/GP code zet ze allemaal op een rijtje. q=partitions(7); c=0; for(i=1,#q, z=q[i]; f=1; for(j=1,#z-1, if(z[j]==z[j+1], f*=0));if(f, c++; print(c," ",q[i]))) | 5.68 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Optellen = vermenigvuldigen \({\Large\frac{5}{2}}+{\Large\frac{5}{3}} = {\Large\frac{5}{2}}*{\Large\frac{5}{3}}\) | 5.69 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(twee multigrades) \(5\to5^5\to\) \begin{aligned} 5^1&=-101^1-249^1+358^1+755^1-758^1\\ 5^5&=-101^5-249^5+358^5+755^5-758^5\\ \\ 5^1&=-131^1-609^1+805^1+929^1-989^1\\ 5^5&=-131^5-609^5+805^5+929^5-989^5\\ \end{aligned} | 5.70 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Als \(n\) een priemgetal is verschillend van \(\large\color{blue}{5}\), dan is \(n\) een deler van \(F_{n-1}\) OF van \(F_{n+1}\). \(F_n\) staat voor het \(n\)de Fibonacci getal. Voorbeeld : Priemgetal \(307\) deelt ofwel \(F_{306}\) ofwel \(F_{308}\). \(\require{cancel}{307~\cancel{\;|\;}~{\color{red}{F_{306}}}=3987795824799770715342824788687062628452272409956636682999616408}\) \(307~\;|\;~{\color{green}{F_{308}}}=10440185009520720572083697583620800653786381708749108822250120621\) | 5.71 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(5\) is het tweede Fermat priemgetal \(\to2^{2^1}+1~~\) (OEIS A019434) | 5.72 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\(5\mathbf{\color{blue}{\;=\;}}6^2+15^2-16^2\mathbf{\color{blue}{\;=\;}}6+15-16\) \(5\mathbf{\color{blue}{\;=\;}}7^2+10^2-12^2\mathbf{\color{blue}{\;=\;}}7+10-12\) | 5.73 |