Introduction
Palindromic numbers are numbers which read the same from
left to right (forwards) as from the right to left (backwards)
An Animated Example
 |
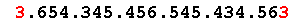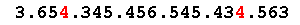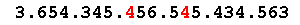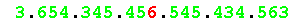Triangular numbers are defined and calculated by this extraordinary intricate and excruciatingly complex formula.
So, this line is for experts only 
base x ( base + 1 )
------------------------or( base 2 + base ) / 2
2
|
Normal and Palindromic Triangulars
So far this compilation counts 195 palindromic triangulars.
Here is the largest Triangular Palindrome that Patrick De Geest
discovered, using CUDA code by Robert Xiao, on [ September 18, 2023 ].
This basenumber
11.604.355.897.766.717.137.264.209.814.751
has 32 digits
yielding the following palindromic triangular record number
67.330.537.901.016.595.837.936.819.195.144.159.191.863.973.859.561.010.973.503.376
with a length of 62 digits.
|
This world record was achieved using CUDA code written by Robert Xiao and no longer
on Rust. Recently he generalized the program to handle arbitrary quadratics.
CUDA is a programming language, or more properly a programming toolkit,
for writing software to run on GPUs rather than CPUs. It runs about 50 times faster on our
GPUs though the logic of the code follows the Rust version closely.
I asked Robert now that his CUDA is running at warp speed how far it would reach.
He answered that as for 70 digits the time estimate on that is around ~400 days on one of
our GPUs. 60 digits is about two days of GPU time, and it’ll go up by a factor of 10 every 4 digits.
Doable but it’ll be a pretty decent power bill :) “Maybe we could get some palindrome enthusiasts
together”, as David Griffeath put it, “and get a distributed computation going.”
The program is very amenable to divide-and-conquer approaches.
|
Triangular numbers, whether palindromic or not, can only end with the following digits 0, 1, 3, 5, 6 or 8.
Alas, my palindromes may not have leading 0's! So the zero option must not be investigated.
1 can be followed by any number : 10, 11, 12, 13, 14, 15, 16, 17, 18 or 19
3 can only be followed by 0 or 5 : 35 or 35
5 can be followed by any number : 50, 51, 52, 53, 54, 55, 56, 57, 58 or 59
6 can be followed by any number : 60, 61, 62, 63, 64, 65, 66, 67, 68 or 69
8 can only be followed by 2 or 7 : 82 or 87
There exist no palindromic triangulars of length 12, 30, 40, 47, 48, 50, 56, 60.
| Case Triangle | Change of variables | CUDApalin parameters | Base Correction |
| odd base | n = 2 * m + 1 | A B C → 2 3 1 | CUDAbase * 2 + 1 |
| even base ver 1 | n = 2 * m | A B C → 2 1 0 | CUDAbase * 2 |
| even base ver 2 | n = 2 * m + 2 | A B C → 2 5 3 | CUDAbase * 2 + 2 |
Every hexagonal number is a triangular number.
A good source for such statements is
“The Book of Numbers”
by
John H. Conway and
Richard K. Guy.
Click on the image on the left for more background about the book.
The book can be ordered at 'www.amazon.com'.
The set of hexagonal numbers is a subset of the triangular numbers.
In fact every other triangular number Tn is a hexagonal number,
with Hn = T2n–1. So in practice this means that whenever you have
an odd basenumber of a triangular (it doesn't matter if it is palindromic
or not) add 1 and divide by 2 and you'll have your basenumber of
a hexagonal number.
For instance BaseT = 3185 gives (3185+1)/2 or BaseH = 1593.
Both basenumbers yield resp. 5073705 ! (See T20 and H13 in the list
of palindromic triangulars and hexagonals.)
The best way to get a 'structural' insight as how to imagine tetrahedrals is to visit these sites :
| Triangular Number | From Eric Weisstein's Math Encyclopedia |
|---|
| Triangles | Acquaint yourself with TRIANGULAR NUMBERS - by Richard Phillips |
|---|
| Amazing Palindromes | Those Amazing Palindromes - by Shareef Bacchus |
|---|
| Entangled | Not all triangles are palindromic, some are... well more entangled ! |
|---|
One can visualize a triangular number as the surface value of an equilateral triangle.
Stick two triangles together so that they form a rectangle and you'll immediately understand the above formula.
Explaining a triangular number in everyday language :
it's the sum of the consecutive integers beginning from 1 up to base.
So, the basenumber is the highest number you add to the sum.
Example (see above figure) : 1 + 2 + 3 + (base = 4) gives the triangular number 10, the total of all 
stars.
Second example : base = 101 gives the triangular number 5151.
The triangular numbers (1,3,6,10,15,...) can be found in the famous Pascal's Triangle.
They appear in the third row like this :
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1 |
Worthwhile links :
|
Bright S. Jaja (email) a sophomore student from Madison, Wisconsin
remarked [ September 28, 1999 ] the following interesting relation between
the five first rows of the Pascal's Triangle and the powers of 11.
110 = 1
111 = 11
112 = 121
113 = 1331
114 = 14641
However, the pattern doesn't continue after this !
José Antônio Fabiano Mendes (email) from Rio de Janeiro, Brazil
counters the above observation [ January 26, 2000 ].
Jaja's remark will always be true if we disregard the carry-1 rule, namely:
1 4 6 4 1 x 11 = 1 5 10 10 5 1
1 5 10 10 5 1 x 11 = 1 6 15 20 15 6 1
and so on ...
Here we are not using the base 10 but an infinite base, so to speak.
Marc Jacobs (email) from Burbank, California [ November 9, 2001 ]
thinks that the 11n pattern does continue past 114 in Pascal's Triangle,
but in a convoluted manner, not quite like José's:
115 = 161051 -- the 5th row says: 1 5 10 10 5 1
now here's where the trickery comes in...
start by keeping the last three digits: 051
add the next digits together in pairs, from right to left:
1 + 0 (from the two 10s) = 1
1 + 5 (from 10) = 6
and the first number: 1
string it all together -- 161051 !
116 = 1771561 -- the 6th row says: 1 6 15 20 15 6 1
start by keeping the last three digits: 561
add the next digits together in pairs, from right to left:
1 + 0 = 1
2 + 5 = 7
1 + 6 = 7
and the first number: 1
string it all together -- 1771561
117 = 19487171 -- the 7th row says: 1 7 21 35 35 21 7 1
start by keeping the last three digits: 171
2 + 5 = 7
3 + 5 = 8
3 + 1 = 4
2 + 7 = 9
and the first number: 1
string it all together -- 19487171
Now it gets a bit trickier - it involves carrying:
118 = 214358881 -- the 8th row says: 1 8 28 56 70 56 28 8 1
start by keeping the last three digits: 881
now work from right to left, adding pairs and carrying:
2 + 6 = 8
5 + 0 = 5
7 + 6 = 13 (keep 3, carry 1 to next pair)
5 + 8 = 13 + 1 = 14 (keep 4, carry 1 to next pair)
2 + 8 = 10 + 1 = 11 (keep 1, carry 1)
the first 1 + the carried 1 = 2
string it all together -- 214358881
3 digit numbers in the triangle mean we add them as 2 digit numbers:
119 = 2357947691 -- the 9th row says: 1 9 36 84 126 126 84 36 9 1
start by keeping the last three digits: 691
3 + 4 = 7
8 + 6 = 14 (keep 4, carry 1)
12 + 6 = 18 + 1 = 19 (keep 9, carry 1)
12 + 4 = 16 + 1 = 17 (keep 7, carry 1)
8 + 6 = 14 + 1 = 15 (keep 5, carry 1)
3 + 9 = 12 + 1 = 13 (keep 3, carry 1)
the first 1 + the carried 1 = 2
string it all together -- 2357947691
Good luck with higher numbers!
But I don't see any reason why this shouldn't continue in this manner.
Thanks,
Marc, for this new insight into the continuation of the
11n palindromic patterns.
Sloane's A001110 gives the first numbers that are both Triangular and Square.
1, 36, 1225, 41616, 1413721, 48024900, ...
Check out also Sloane's entries A001108 and A001109 to discover more about the topic.
Relationship between Triangular and Square Numbers
Square and Triangular numbers
From Eric Weisstein's Math Encyclopedia : Triangular Square Number
Here is a formula that generates these numbers which are both triangular and square.
It is written in the UBASIC syntax :
10 for N=1 to 9
20 X=ceil(((17+12*sqrt(2))^N+(17-12*sqrt(2))^N-2)/32)
30 print N,X
40 next N
Sloane's A014979 gives the first numbers that are both Triangular and Pentagonal.
(Sequence corrected and extended by Warut Roonguthai (email).)
1, 210, 40755, 7906276, 1533776805, 297544793910, ...
Consult also Eric Weisstein's page Triangular Pentagonal Number.
Sloane's A046194 gives the first numbers that are both Triangular and Heptagonal.
1, 55, 121771, 5720653, 12625478965, ...
Consult also Eric Weisstein's page Triangular Heptagonal Number.
Sloane's A046183 gives the first numbers that are both Triangular and Octagonal.
1, 21, 11781, 203841, 113123361, ...
Consult also Eric Weisstein's page Triangular Octagonal Number.
Sloane's A048909 gives the first numbers that are both Triangular and Nonagonal.
1, 325, 82621, 20985481, 5330229625, 1353857339341,...
Consult also Eric Weisstein's page Triangular Nonagonal Number.
Another interesting entry from Sloane's table is :
%N Doubly triangular numbers: C(n+2,2)+3C(n+3,4). under A002817
Michael Mann (email)
found an interesting way to construct the first few triangular numbers...
If you write how many 3-digit numbers have 0,1,2,3,4,... as a sum of their digits,
you will get the sequence of the triangular numbers.
This means any number which can be represented using three decimal positions
(say 10 = 010), i.e. those that have ⩽ 3 digits.
Consider these numbers :
how many have 0 as a sum of their digits -- 1 (0)
sum 1 -- 3 numbers (1, 10, 100)
sum 2 -- 6 (2, 20, 200, 11, 110, 101)
sum 3 -- 10 (3, 30, 300, 21, 12, 102, 201, 111, 120, 210)
sum 4 -- 15 (4, 40, 400, 31, 13, 130, 310, 301, 103, 202, 22, 220, 211, 212, 122)
sum 5 -- 21 (32, 23, 203, 302, ...)
etc.
It is just easier to count the numbers with particular sum of the digits by representing
each number in 3 decimal positions : say, for sum 3 :
C(3, 1) //those which have only 3 in them, 3, 30, 300
C(3, 1)*C(2, 1) //those which have one 2 and one 1 in them 210, 021, 120 etc.
C(3, 3) //those that have 3 ones in them
It looks like the sequence produced is a part of triangular numbers sequence.
I don't know what the exact explanation for it is.
If you have one couldn't you share it ?
Michael Mann's own reply [ July 31, 2000 ]
Michael thought more about it himself in the following days
and realised that his conjecture is true only for Sum ⩽ 9.
Here is his proof why it is true only for the small values : for Sum ⩽ 9.
The number of ⩽ 3 digit number corresponding to each value of the Sum is the
number of ways to put Sum non-distinguishable items into 3 distinguishable
boxes where each box can hold 0 ⩽ n ⩽ Sum items.
= C(n+2, 2) = C(n+2, n) = (n+1) + n*(n-1)/2 -- a triangular number.
So it is just a matter of
C(i, 2) being a triangular number.
Unfortunately in case of representation as a decimal number it holds for ⩽ 9 only.
Statistics with focus starting from Triangular Palindromes lengths
TP = Triangular Palindromes
| | Triangular Palindrome_(TP)_length | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |
|---|
A054263
A307367 | # TP's | 3
4 | 2 | 3 | 3 | 2 | 2 | 6 | 2 | 1 | 4 | 7 | 0 | 4 | 4 | 12 | 5 | 6 | 2 | 3 | 2 | 6 | 3 | 6 | 2 | 2 | 4 | 3 | 2 | 5 | 0 | 3 | 2 | 1 | 4 | 3 |
|---|
| | sector [0...0] & [1...1] | 2 | 0 | 1 | 0 | 1 | 0 | 2 | 0 | 1 | 2 | 2 | 0 | 1 | 1 | 1 | 3 | 3 | 0 | 0 | 1 | 2 | 2 | 0 | 1 | 0 | 1 | 0 | 1 | 2 | 0 | 0 | 1 | 0 | 0 | 0 |
|---|
| | sector [30...03] | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
|---|
| | sector [35...53] | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
|---|
| | sector [5...5] | 0 | 1 | 1 | 1 | 0 | 0 | 2 | 0 | 0 | 1 | 2 | 0 | 2 | 0 | 4 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 2 | 0 |
|---|
| | sector [6...6] | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 2 | 6 | 1 | 2 | 0 | 1 | 1 | 1 | 0 | 2 | 0 | 0 | 1 | 1 | 0 | 2 | 0 | 1 | 0 | 0 | 1 | 2 |
|---|
| | sector [82...28] | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
|---|
| | sector [87...78] | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|
| |
| Continued... | Triangular Palindrome_(TP)_length | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
|---|
A054263
A307367 | # TP's | 1 | 10 | 1 | 4 | 0 | 3 | 2 | 2 | 1 | 3 | 3 | 0 | 0 | 9 | 0 | 3 | 2 | 4 | 3 | 5 | 0 | 4 | 2 | 2 | 0 | 4 | 7 | - | - | - | - | - | - | - | - |
|---|
| | sector [1...1] | 0 | 1 | 0 | 2 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 4 | 0 | 1 | 2 | 3 | 2 | 3 | 0 | 1 | 1 | 0 | 0 | 2 | 3 | - | - | - | - | - | - | - | - |
|---|
| | sector [30...03] | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | - | - | - | - | - | - | - | - |
|---|
| | sector [35...53] | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | - | - | - | - | - | - | - | - |
|---|
| | sector [5...5] | 0 | 4 | 0 | 1 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 2 | 0 | 0 | 0 | - | - | - | - | - | - | - | - |
|---|
| | sector [6...6] | 0 | 3 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 3 | - | - | - | - | - | - | - | - |
|---|
| | sector [82...28] | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | - | - | - | - | - | - | - | - |
|---|
| | sector [87...78] | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | - | - | - | - | - | - | - | - |
|---|
Palindromic Triangulars
Neil Sloane's “Integer Sequences” Encyclopedia can be consulted online :
Neil Sloane's Integer Sequences
The following two triangular sequences are already categorised.
%N Triangular numbers: n(n+1)/2. under A000217
%N Palindromic triangular numbers. under A003098.
I added the following sequences :
%N nth triangular number is palindromic. under A008509
%N Both n and nth triangular number are palindromes. under A008510
%N Number of palindromic triangular numbers with n digits. under A054263
Click here to view some of the author's [P. De Geest] entries to the table.
Click here to view some entries to the table about palindromes.
|
Normal basenumbers and their palindromic triangular numbers 
two examples:
11088 gives us 61477416.
109656228 results in 6012244224422106.
In some cases the basenumbers are themselves palindromic! two examples:
363474363 results in 66056806460865066.
266444444662 results in 35496321045754012369453.
Can you think of more beautiful and mind-boggling numbers...
As it turns out, these numbers are extremely rare and hard to find.
Please inform me if you know more palindromic triangulars
or whether you're about to challenge me by trying to extend the list.
You'll find my e-mail address at the bottom of this page.
Of this collection a subset of only 19 are themselves palindromic !
The "palindromic triangular with a palindromic basenumber" record holder is [131]
3654345456545434563
6677120357887130286820317887530217766
Even more scarcely distributed are the palindromic triangulars with a prime basenumber.
A mere eight of these special triangulars could be added in the 'subsets'-table section.
Btw the triangular numbers larger than 3 are always composite of course.
The largest one known to this day is [p1]
5510313150359237826498809954773
15181775507510974169398336861133116863389396147901570557718151
Results from investigating these numbers
Highlighting out extra characteristics or relationships
about the PALINDROMIC TRIANGULARS
is a way to give these numbers added value. Some can be quite obvious as others can be more elaborate
or even far-fetched. There's almost no limit in what you can find out. While extending the list
with the next higher palindromic triangular may be very difficult to accomplish, searching
for extra features in the existing ones is something that we all could embark on.
“ The only limitation is one's imagination ” as the saying goes.
To give you an idea I'll show you some results of my own humble investigations.
If you consult the full listing of the palindromic triangulars you'll see
a column with the hypertext word 'Info'. This will lead you to a new page
displaying additional information about the referenced triangulars.
Things like prime factors, number-lengths, discovery dates, features, comments... can be
found there. My first idea was to incorporate them also in the table,
but that would have lead to an overloaded table difficult to manage. ↓ Some random excerpts ↓
I found FOUR YEARS IN A ROW in the following palindromic triangulars !
Will these be the most prolific years of my life ?
[122] 1873574437207991455541997027344753781
[73] 15199896744769899151
[116] 5952926739999190550919999376292595
[40] 6874200024786
The 'smallest' triangular number with FOUR digit 8's in its decimal expansion is palindromic !
[16] 828828
[See Sloane A036525]
The sum of the first thirteen triangle basenumbers is itself palindromic
1 + 2 + 3 + 10 + 11 + 18 + 34 + 36 + 77 + 109 + 132 + 173 + 363 = 969
The last palindromic basenumber 363 can be expressed as the sum of consecutive powers of the base 3
[14] 363 = 31 + 32 + 33 + 34 + 35
All the EVEN palindromic triangulars carry the factor 11 in their genes.
This number 11 is itself a palindromic basenumber, refer to [6].
And 11 is the only existing palindromic prime with an 'even' number of digits.
Dividing into groups of three :
[106] 353.520.620.692.923 equals A.B.C.D.E
( A + B + C + D + E ) = 3108
Just a number like any other, where it not for the property that 3108 is the sum of seven repdigital palindromes :
111 + 222 + 333 + 444 + 555 + 666 + 777 = 7 x 444
Creating “a triplet of duo's ” is another way to split this one up :
(35)(35)_(206)(206)_(92)(92)__(3)
By the way summing up all three pairs generates the number of the beast nl. 666.
I found that the beast's number pops up in more than one palindromic triangular (see for instance [9]). So be warned...
[31] 179.158 equalling A.B
( A x B ) = 179 x 158 = 28282. Palindromes creep up in many unexpecting ways !
Here's the INTEL triangular love affair :
[54] 681909070909186
[55] 683727232727386
[56] 684866959668486 ¿ So, what happened with the 286 ?
Four is a rewarding number when dealing with palindromic triangulars as e.g. when groupings of four are summed up in :
[121] 300721668093919607706919390866127003
Nine groups of four looks like : 3007 + 2166 + 8093 + 9196 + (0)770 + 6919 + 3908 + 6612 + 7003
And yes, after adding them together... you've guessed it : a palindrome shows up : 47674
Consider its basenumber for a moment : 775.527.779.120.670.322
where the extraction of the middle digits of the six trio's reveals this nice undulating pattern 7.2.7.2.7.2
Add up the numbercouples surrounding these middle digits :
7_5 + 5_7 + 7_9 + 1_0 + 6_0 + 3_2 = 313 again a palindromic number.
Some triangular numbers have close family ties.
They share the same starting and ending sequence.
[35] 66771917766
[53] 667784464487766
[99] 667712035788060887530217766
[131] 6677120357887130286820317887530217766
or
[29] 61728-82716
[42] 61728399382716
That a similar nonpalindromic pattern exists with some basenumbers is quite unexpected :
[26] 50281
[57] 50008881
[101] 50364608806281
Do you like this peculiar pattern starting with prime number 109 ?
The length of each basenumber is always a multiple of three !
[11] 109
[60] 109656228
[102] 109237730189290
[116] 109113947229482909
The next triangular consists only of the odd digits 1, 3, 5 and 9 :
[48] 539593131395935
The next triangular consists only of the even digits 0, 2, 6 and 8 :
[61] 8208268228628028
There are a few beautiful basenumbers composed only of the digits 3, 4, 5 and 6.
They seem to grow like crystals.
[4] 3
[9] 36
[14] 363
[35] 365436
[50] 34456434
[53] 36545436
[99] 36543454565436
[131] 3654345456545434563 - Most beautiful palindromic triangular
This palindromic basenumber [71] 2664444662 has exactly three palindromic factors !
And above all, it only needs the digits 1 and 2 to show them !
2
11
121111121
Thousand reasons to divide these palindromic numbers into blocks of three :
[19] 003 + 544 + 453 = 1000
[26] 001 + 264 + 114 + 621 = 1000
[27] 001 + 634 + 004 + 361 = 1000
DID YOU KNOW ?
There exist a sequence of precisely 1000 digits which includes all the numbers of 1 to 1000 as substrings.
Starting numbers predicting the end... that must be the end !
[74] 11151642876
( 1 + 1 + 1 + 5 ) ( 1 + 6 ) ( 4 + 2 ) = (8) (7) (6) = ..876.
Sources Revealed
“The Penguin Dictionary of Curious and Interesting Numbers” by David Wells - [isbn 0-14-008029-5]
On page 93 one can read :
"Charles Trigg gives examples of palindromic triangular numbers.
There are 40 palindromic triangular numbers below 10^7. The smallest, apart
from 1, 3 and 6, are 55, 66, 171, 595, 666 and 3003. T{2662} = 3544453,
so the number itself and its index, 2662, are both palindromic.
T{1111} and T{111111} are 617716 and 6172882716 respectively."
On page 185 we read about the number 828828 :
"The only triangular palindrome, apart from 55, 66 and 666." !?
My list with more than hundred examples proves overwhelmingly that Mr. Wells is wrong on this point.
More Integer Sequences from Sloane's OEIS Database
- A068641 Smallest n-digit palindromic triangular number. If no such number exists then 0. - Amarnath Murthy
- A068642 Index of the smallest n-digit palindromic triangular number. If no such number exists then 0. - Amarnath Murthy
- A068643 Largest n-digit palindromic triangular number. If no such number exists then 0. - Amarnath Murthy
- A068644 Index of the largest n-digit palindromic triangular number. If no such number exists then 0. - Amarnath Murthy
[
TOP OF PAGE]